
【题目】阅读理解材料一:一组对边平行,另一组对边不平行的四边形叫梯形,其中平行的两边叫梯形的底边,不平行的两边叫梯形的底边,不平行的两边叫梯形的腰,连接梯形两腰中点的线段叫梯形的中位线.梯形的中位线具有以下性质:梯形的中位线平行于两底和,并且等于两底和的一半.
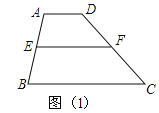
如图(1):在梯形ABCD中:AD∥BC,
∵E、F是AB、CD的中点,∴EF∥AD∥BC,EF=![]() (AD+BC)
(AD+BC)
材料二:经过三角形一边的中点与另一边平行的直线必平分第三边
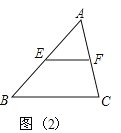
如图(2):在△ABC中:∵E是AB的中点,EF∥BC
∴F是AC的中点
请你运用所学知识,结合上述材料,解答下列问题.
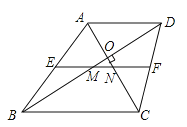
如图(3)在梯形ABCD中,AD∥BC,AC⊥BD于O,E、F分别为AB、CD的中点,∠DBC=30°.
(1)求证:EF=AC;
(2)若OD=![]() ,OC=5,求MN的长.
,OC=5,求MN的长.
【答案】(1)证明见试题解析;(2)2.
【解析】
(1)由直角三角形中30°的锐角所对的直角边是斜边的一半,可得OA=![]() AD,OC=
AD,OC=![]() BC,即可证明;
BC,即可证明;
(2)直角三角形中30°的锐角所对的直角边是斜边的一半,得出OA=3,利用平行线得出ON=![]() MN,再根据AN=
MN,再根据AN=![]() AC=4,得出ON=4﹣3=1,进而得出MN的值.
AC=4,得出ON=4﹣3=1,进而得出MN的值.
解:(1)∵AD∥BC,∴∠ADO=∠DBC=30°,∴在Rt△AOD和Rt△BOC中,OA=![]() AD,OC=
AD,OC=![]() BC,∴AC=OA+OC=
BC,∴AC=OA+OC=![]() (AD+BC),∵EF=
(AD+BC),∵EF=![]() (AD+BC),∴AC=EF;
(AD+BC),∴AC=EF;
(2)∵AD∥BC,∴∠ADO=∠DBC=30°,∴在Rt△AOD和Rt△BOC中,OA=![]() AD,OC=
AD,OC=![]() BC,∵OD=
BC,∵OD=![]() ,OC=5,∴OA=3,∵AD∥EF,∴∠ADO=∠OMN=30°,∴ON=
,OC=5,∴OA=3,∵AD∥EF,∴∠ADO=∠OMN=30°,∴ON=![]() MN,∵AN=
MN,∵AN=![]() AC=
AC=![]() (OA+OC)=4,∴ON=AN﹣OA=4﹣3=1,∴MN=2ON=2.
(OA+OC)=4,∴ON=AN﹣OA=4﹣3=1,∴MN=2ON=2.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
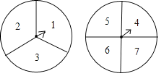
【题目】两个自由转动的转盘如图所示,一个分为![]() 等份,分别标有数字
等份,分别标有数字![]() ,
,![]() ,
,![]() ,另一个分为
,另一个分为![]() 等份,分别标有数字
等份,分别标有数字![]() ,
,![]() ,
,![]() ,
,![]() .转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面
.转盘上有固定指针,同时转动两个转盘,当转盘停止转动后,指针指向的数字即为转出的数字.甲、乙两人制定游戏规则如下:一人先猜数,然后另一人再转动转盘,若猜出的数字与转出的两个数字之和相等,则猜数的人获胜,否则转动转盘的人获胜.猜数者可从下面![]() ,
,![]() 两种方案中选一种:方案
两种方案中选一种:方案![]() :猜“奇数”或猜“偶数”其中的一种;方案
:猜“奇数”或猜“偶数”其中的一种;方案![]() :猜“是
:猜“是![]() 的整数倍”或猜“不是
的整数倍”或猜“不是![]() 的整数倍”其中的一种.
的整数倍”其中的一种.
![]() 如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种方案,猜该种方案中的哪一种情况?请说明理由;
如果你是猜数的游戏者,为了尽可能获胜,你将选择哪种方案,猜该种方案中的哪一种情况?请说明理由;
![]() 为了保证参与游戏双方的公平性,你应选择哪种猜数的方案?为什么?
为了保证参与游戏双方的公平性,你应选择哪种猜数的方案?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一座人行天桥的示意图,天桥的高度是10米,CB⊥DB,坡面AC的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面DC的坡度为i=![]() :3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据:
:3.若新坡角下需留3米宽的人行道,问离原坡角(A点处)10米的建筑物是否需要拆除?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
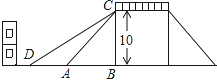
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将量角器和含![]() 角的一块直角三角板紧靠着放在同一平面内,使
角的一块直角三角板紧靠着放在同一平面内,使![]() ,
,![]() ,
,![]() 在一条直线上,且
在一条直线上,且![]() ,过点
,过点![]() 作量角器圆弧所在圆的切线,切点为
作量角器圆弧所在圆的切线,切点为![]() ,如果
,如果![]() ,则
,则![]() 的长是________
的长是________![]() .
.
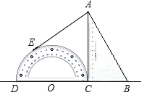
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列事件发生的概率标在图1中(用字母表示):
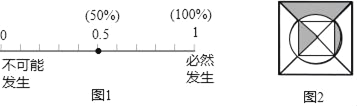
(1)记为点A:随意掷两枚质地均匀的骰子,朝上面的点数之和为1;
(2)记为点B:抛出的篮球会下落;
(3)记为点C:从装有3个红球、7个白球的口袋中任取一个球,恰好是白球(这些球除颜色外完全相同);
(4)记为点D:如图2所示的正方形纸片上做随机扎针实验,则针头恰好扎在阴影区域内.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2017甘肃省天水市)△ABC和△DEF是两个全等的等腰直角三角形,∠BAC=∠EDF=90°,△DEF的顶点E与△ABC的斜边BC的中点重合,将△DEF绕点E旋转,旋转过程中,线段DE与线段AB相交于点P,线段EF与射线CA相交于点Q.
(1)如图①,当点Q在线段AC上,且AP=AQ时,求证:△BPE≌△CQE;
(2)如图②,当点Q在线段CA的延长线上时,求证:△BPE∽△CEQ;并求当BP=2,CQ=9时BC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=10,AC=8,BC=6,以边AB的中点O为圆心,作半圆与AC相切,点P,Q分别是边BC和半圆上的动点,连接PQ,则PQ长的最小值是_______.
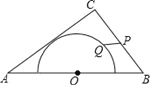
查看答案和解析>>
科目:初中数学 来源: 题型:
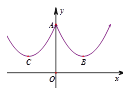
【题目】如图4所示的是桥梁的两条钢缆具有相同的抛物线形状.按照图中建立的直角坐标系,右面的一条抛物线的解析式为y=x2-4x+5表示,而且左右两条抛物线关于y轴对称,则左面钢缆的表达式为_________________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
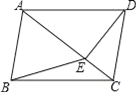
【题目】如图,在四边形ABCD中,AB∥CD,∠ABC=∠ADC,DE垂直于对角线AC,垂足是E,连接BE.
(1)求证:四边形ABCD是平行四边形;
(2)若AB=BE=2,sin∠ACD=![]() ,求四边形ABCD的面积.
,求四边形ABCD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com