
【题目】交通工程学理论把在单向道路上行驶的汽车看成连续的流体,并用流量、速度、密度三个概念描述车流的基本特征,其中流量![]() (辆
(辆![]() 小时)指单位时间内通过道路指定断面的车辆数;速度
小时)指单位时间内通过道路指定断面的车辆数;速度![]() (千米
(千米![]() 小时)指通过道路指定断面的车辆速度,密度
小时)指通过道路指定断面的车辆速度,密度![]() (辆
(辆![]() 千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量
千米)指通过道路指定断面单位长度内的车辆数.为配合大数据治堵行动,测得某路段流量![]() 与速度
与速度![]() 之间关系的部分数据如下表:
之间关系的部分数据如下表:
速度v(千米/小时) |
|
|
|
|
|
|
|
|
流量q(辆/小时) |
|
|
|
|
|
|
|
|
(1)根据上表信息,下列三个函数关系式中,刻画![]() ,
,![]() 关系最准确是_____________________.(只填上正确答案的序号)
关系最准确是_____________________.(只填上正确答案的序号)
①![]() ;②
;②![]() ;③
;③![]()
(2)请利用(1)中选取的函数关系式分析,当该路段的车流速度为多少时,流量达到最大?最大流量是多少?
(3)已知![]() ,
,![]() ,
,![]() 满足
满足![]() ,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当
,请结合(1)中选取的函数关系式继续解决下列问题:市交通运行监控平台显示,当![]() 时道路出现轻度拥堵.试分析当车流密度
时道路出现轻度拥堵.试分析当车流密度![]() 在什么范围时,该路段将出现轻度拥堵?
在什么范围时,该路段将出现轻度拥堵?
【答案】(1)答案为③;(2)v=30时,q达到最大值,q的最大值为1800;(3)84<k≤96
【解析】
(1)根据一次函数,反比例函数和二次函数的性质,结合表格数据,即可得到答案;
(2)把二次函数进行配方,即可得到答案;
(3)把v=12, v=18,分别代入二次函数解析式,求出q的值,进而求出对应的k值,即可得到答案.
(1)∵![]() ,q随v的增大而增大,
,q随v的增大而增大,
∴①不符合表格数据,
∵![]() ,q随v的增大而减小,
,q随v的增大而减小,
∴②不符合表格数据,
∵![]() ,当q≤30时,q随v的增大而增大,q≥30时,q随v的增大而减小,
,当q≤30时,q随v的增大而增大,q≥30时,q随v的增大而减小,
∴③基本符合表格数据,
故答案为:③;
(2)∵q=﹣2v2+120v=﹣2(v﹣30)2+1800,且﹣2<0,
∴当v=30时,q达到最大值,q的最大值为1800.
答:当该路段的车流速度为30千米/小时,流量达到最大,最大流量是1800辆/小时.
(3)当v=12时,q=﹣2×122+120×12=1152,此时k=1152÷12=96,
当v=18时,q=﹣2×182+120×18=1512,此时k=1512÷18=84,
∴84<k≤96.
答:当84<k≤96时,该路段将出现轻度拥堵.


科目:初中数学 来源: 题型:
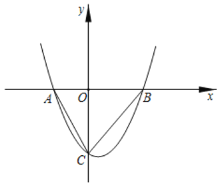
【题目】已知抛物线y=ax2+bx+c经过点A(﹣2,0),B(3,0),与y轴负半轴交于点C,且OC=OB.
(1)求抛物线的解析式;
(2)在y轴负半轴上存在一点D,使∠CBD=∠ADC,求点D的坐标;
(3)点D关于直线BC的对称点为D′,将抛物线y=ax2+bx+c向下平移h个单位,与线段DD′只有一个交点,直接写出h的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
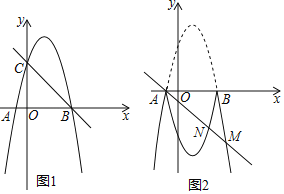
【题目】如图1,二次函数y=ax2﹣3ax+c的图象与x轴交于点A、B,与y轴交于点c直线y=﹣x+4经过点B、C.
(1)求抛物线的表达式;
(2)过点A的直线y=kx+k交抛物线于点M,交直线BC于点N,连接AC,当直线y=kx+k平分△ABC的面积,求点M的坐标;
(3)如图2,把抛物线位于x轴上方的图象沿x轴翻折,当直线y=kx+k与翻折后的整个图象只有三个交点时,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
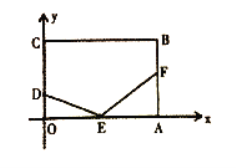
【题目】如图,在平面直角坐标系中,点![]() ,过点
,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() .作
.作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() 点
点![]() 从
从![]() 出发,沿
出发,沿![]() 轴正方向以每秒
轴正方向以每秒![]() 个单位长度运动;点
个单位长度运动;点![]() 从
从![]() 出发,沿
出发,沿![]() 轴正方向以每秒
轴正方向以每秒![]() 个单位长度运动;点
个单位长度运动;点![]() 从
从![]() 出发,沿
出发,沿![]() 方向以每秒
方向以每秒![]() 个单位长度运动.当
个单位长度运动.当![]() 点运动到点
点运动到点![]() 时,三点随之停止运动.设运动时间为
时,三点随之停止运动.设运动时间为![]() .
.
(1)用含![]() 的代数式分别表示点
的代数式分别表示点![]() ,点
,点![]() 的坐标.
的坐标.
(2)若![]() 与以点
与以点![]() ,
,![]() ,
,![]() 为顶点的三角形相似,求
为顶点的三角形相似,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,动点
,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;同时,动点
;同时,动点![]() 从点
从点![]() 出发,沿
出发,沿![]() 方向匀速运动,速度为
方向匀速运动,速度为![]() ;当一个点停止运动,另一个点也停止运动.设点
;当一个点停止运动,另一个点也停止运动.设点![]() ,
,![]() 运动的时间是
运动的时间是![]()
![]()
![]() .过点
.过点![]() 作
作![]() 于点
于点![]() ,连接
,连接![]() ,
,![]() .
.
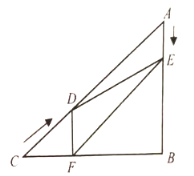
(1)![]() 为何值时,
为何值时,![]() ?
?
(2)设四边形![]() 的面积为
的面积为![]() ,试求出
,试求出![]() 与
与![]() 之间的关系式;
之间的关系式;
(3)是否存在某一时刻![]() ,使得
,使得![]() 若存在,求出
若存在,求出![]() 的值;若不存在,请说明理由;
的值;若不存在,请说明理由;
(4)当![]() 为何值时,
为何值时,![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分10分)(1)问题发现
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE,
填空:①∠AEB的度数为 ;
②线段AD、BE之间的数量关系是 .
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=900, 点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.请判断∠AEB的度数及线段CM、AE、BE之间的数量关系,并说明理由.


(3)解决问题如图3,在正方形ABCD中,CD=![]() .若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.
.若点P满足PD=1,且∠BPD=900,请直接写出点A到BP的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂设计了一款成本为20元/件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | … | 30 | 40 | 50 | 60 | … |
每天销售量 | … | 500 | 400 | 300 | 200 | … |
(1)研究发现,每天销售量![]() 与单价
与单价![]() 满足一次函数关系,求出
满足一次函数关系,求出![]() 与
与![]() 的关系式;
的关系式;
(2)当地物价部门规定,该工艺品销售单价最高不能超过45元/件,那么销售单价定为多少时,工艺厂试销该工艺品每天获得的利润8000元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】省射击队为从甲、乙两名运动员中选拔一人参加全国比赛,对他们进行了六次测试,测试成绩如下表(单位:环):
第一次 | 第二次 | 第三次 | 第四次 | 第五次 | 第六次 | |
甲 | 10 | 8 | 9 | 8 | 10 | 9 |
乙 | 10 | 10 | 10 | 9 | 8 |
(1)根据表格中的数据,可计算出甲的平均成绩是 环(直接写出结果);
(2)已知乙的平均成绩是9环,试计算其第二次测试成绩的环数;
(3)分别计算甲、乙六次测试成绩的方差,根据计算的结果,你认为推荐谁参加全国比赛更合适,请说明理由.
(计算方差的公式:![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com