

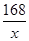 ����ʱx�ķ�Χ��x��6��
����ʱx�ķ�Χ��x��6��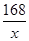 ��x=14����Ըò��Ͻ�����������õ�ʱ��Ϊ14��2=12��
��x=14����Ըò��Ͻ�����������õ�ʱ��Ϊ14��2=12��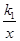 ��
��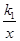 ����12��14������k1=12��14=168��
����12��14������k1=12��14=168��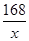 ��
��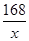 ����x=6��
����x=6��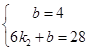 ��
��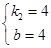 ��
��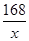 ��ʱx�ķ�Χ��x��6��
��ʱx�ķ�Χ��x��6��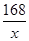 ��x=14��
��x=14��


| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
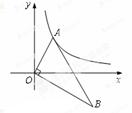
 �ĺ������������غ�����.��
�ĺ������������غ�����.�� ʱ�������غ�����
ʱ�������غ�����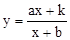 ���Ƿ���������
���Ƿ���������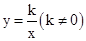 .
.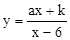 ��ͼ��B��E����.
��ͼ��B��E����. ��ͼ������ƽ��6����λ��������ƽ�� ����λ�Ϳɵõ��������á����غ�������ͼ��.���߶�BE�е�M��һ��ֱ��l����������غ�������ͼ����P��Q���㣬����B��E��P��QΪ������ɵ��ı������Ϊ
��ͼ������ƽ��6����λ��������ƽ�� ����λ�Ϳɵõ��������á����غ�������ͼ��.���߶�BE�е�M��һ��ֱ��l����������غ�������ͼ����P��Q���㣬����B��E��P��QΪ������ɵ��ı������Ϊ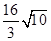 ����ֱ��д����P�����꣮
����ֱ��д����P�����꣮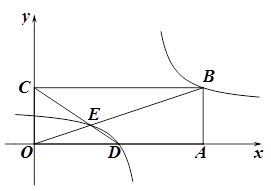
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
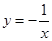 ��ͼ����������
��ͼ����������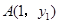 ��
��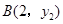 ����
���� ______
______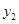 ���
���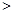 ����
����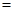 ����
����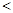 ������
�������鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
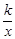 ��ͼ��BC��AB�ڵ�D��E��
��ͼ��BC��AB�ڵ�D��E��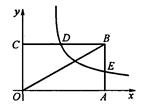
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| x2-1 |
| x2+x |
| x2-1 |
| x |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
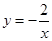 ��������A��x1��y1����B��x2��y2������y1��y2����x1-x2��ֵ�ǣ�������
��������A��x1��y1����B��x2��y2������y1��y2����x1-x2��ֵ�ǣ�������| A������ | B������ | C�������� | D������ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
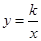 ��k��0��ͼ�������㣬��ֱ��l��ʹA��B��C��ֱ��l�ľ���֮��Ϊ3��1��1��������������ֱ��l���У�������
��k��0��ͼ�������㣬��ֱ��l��ʹA��B��C��ֱ��l�ľ���֮��Ϊ3��1��1��������������ֱ��l���У�������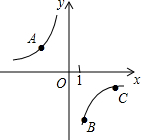
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
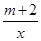 ��ͼ������������y��ֵ��xֵ�������������m��ȡֵ��Χ��(����)
��ͼ������������y��ֵ��xֵ�������������m��ȡֵ��Χ��(����)| A��m����2 | B��m����2 | C��m��2 | D��m��2 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com