
分析 (1)根据平行线的判定方法一一即可解决问题;
(2)欲证明AD=BC,只要证明△ABC≌△BAD即可解决问题;
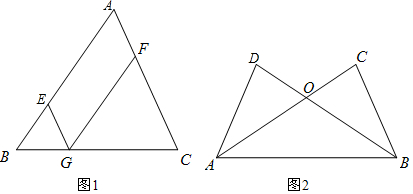
解答 (1)解:如图1,①如果∠B=∠FGC,则 AB∥GF,其理由是(同位角相等两直线平行).
故答案为AB∥FG,同位角相等,两直线平行.
②∠BEG=∠EGF,则AB∥FG,其理由是(内错角相等,两直线平行).
故答案为AB∥FG,内错角相等,两直线平行.
③如果∠AEG+∠EAF=180°,则 AC∥EG,其理由是(同旁内角互补、两直线平行).
故答案为AC∥EG,同旁内角互补,两直线平行.
(2)证明:在△ABC和△BAD中,
$\left\{\begin{array}{l}{AC=BD}\\{∠BAC=∠ABD}\\{AB=BA}\end{array}\right.$,
∴△ABC≌△BAD,
∴BC=AD.
点评 本题考查平行线的判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
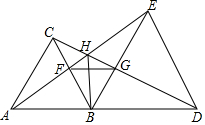 如图,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60°.⑤△BFG是等边三角形,其中正确的有①②④⑤.
如图,已知△ABC和△BDE都是等边三角形.则下列结论:①AE=CD.②BF=BG.③HB⊥FG.④∠AHC=60°.⑤△BFG是等边三角形,其中正确的有①②④⑤.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
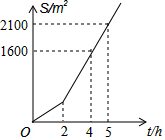 某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )
某社区有一块空地需要绿化,某绿化组承担了此项任务,绿化组工作一段时间后,提高了工作效率,该绿化组完成的绿化面积S(单位:m2)与工作时间t(单位:h)之间的函数关系如图所示,则该绿化组提高工作效率前每小时完成的绿化面积是( )| A. | 500 | B. | 400 | C. | 300 | D. | 200 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com