
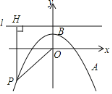
【题目】如图,在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 经过点
经过点![]() ,顶点为点
,顶点为点![]() ,点
,点![]() 为抛物线上的一个动点,
为抛物线上的一个动点,![]() 是过点
是过点![]() 且垂直于
且垂直于![]() 轴的直线,过
轴的直线,过![]() 作
作![]() ,垂足为
,垂足为![]() ,连接
,连接![]() .
.
![]() 求抛物线的解析式,并写出其顶点
求抛物线的解析式,并写出其顶点![]() 的坐标;
的坐标;
![]() ①当
①当![]() 点运动到
点运动到![]() 点处时,计算:
点处时,计算:![]() ________,
________,![]() ________,由此发现,
________,由此发现,![]() ________
________![]() (填“
(填“![]() ”、“
”、“![]() ”或“
”或“![]() ”);
”);
②当![]() 点在抛物线上运动时,猜想
点在抛物线上运动时,猜想![]() 与
与![]() 有什么数量关系,并证明你的猜想.
有什么数量关系,并证明你的猜想.
科目:初中数学 来源: 题型:
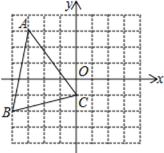
【题目】如图,在下列带有坐标系的网格中,△ABC的顶点都在边长为1的小正方形的顶点上
(1) 直接写出坐标:A__________,B__________
(2) 画出△ABC关于y轴的对称的△DEC(点D与点A对应)
(3) 用无刻度的直尺,运用全等的知识作出△ABC的高线BF(保留作图痕迹)
查看答案和解析>>
科目:初中数学 来源: 题型:
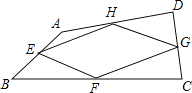
【题目】(满分8分)我们把依次连接任意四边形各边中点得到的四边形叫做中点四边形.
如图,在四边形ABCD中,E、F、G、H分别是AB、BC、CD、DA的中点,依次连接各边中点得到中点四边形EFGH.
(1)这个中点四边形EFGH的形状是____________;
(2)证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某县教育局为了丰富初中学生的大课间活动,要求各学校开展形式多样的阳光体育活动.某中学就“学生体育活动兴趣爱好”的问题,随机调查了本校某班的学生,并根据调查结果绘制成如下的不完整的扇形统计图和条形统计图:

(1)在这次调查中,喜欢篮球项目的同学有 人,在扇形统计图中,“乒乓球”的百分比为 %,如果学校有800名学生,估计全校学生中有 人喜欢篮球项目.
(2)请将条形统计图补充完整.
(3)在被调查的学生中,喜欢篮球的有2名女同学,其余为男同学.现要从中随机抽取2名同学代表班级参加校篮球队,请直接写出所抽取的2名同学恰好是1名女同学和1名男同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
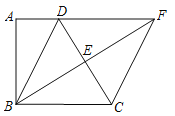
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
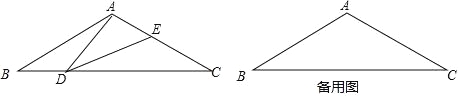
【题目】如图,在等腰三角形ABC中,∠BAC=120°,AB=AC=2,点D是BC边上的一个动点(不与B、C重合),在AC上取一点E,使∠ADE=30°.
(1)求证:△ABD∽△DCE;
(2)设BD=x,AE=y,求y关于x的函数关系式并写出自变量x的取值范围;
(3)当△ADE是等腰三角形时,求AE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com