
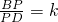 ,是否存在这样的实数k,使得
,是否存在这样的实数k,使得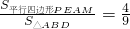 ?若存在,请求出满足条件的所有k的值;若不存在,请说明理由.
?若存在,请求出满足条件的所有k的值;若不存在,请说明理由.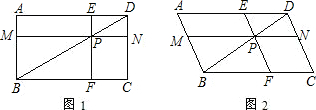
 解:(1)∵ABCD是矩形,
解:(1)∵ABCD是矩形, EH=PE•sin∠MPE,
EH=PE•sin∠MPE,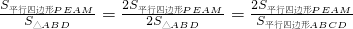 =
= ,
,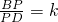 ,即
,即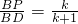 ,
, ,
,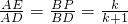 ,
,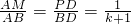 ,
,
 .
. ,使得
,使得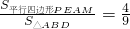 ;
; ,
,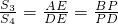
 ∴
∴
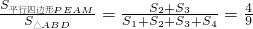


 ,使得
,使得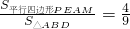 .
.

科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2个 | B、3个 | C、4个 | D、6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
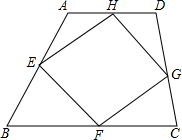 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com