
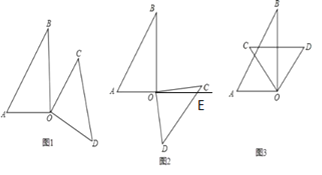
【题目】将一副三角板的直角重合放置,如图1所示,
(1)图1中∠BED的度数为 ;
(2)三角板△AOB的位置保持不动,将三角板△COD绕其直角顶点O顺时针方向旋转:
①当旋转至图2所示位置时,恰好OD∥AB,求此时∠AOC的大小;
②若将三角板△COD继续绕O旋转,直至回到图1位置,在这一过程中,是否会存在△COD其中一边能与AB平行?如果存在,请你画出图形,并直接写出相应的∠AOC的大小;如果不存在,请说明理由.

【答案】(1)15°;(2)①30°;②120°,165°,30°,150°,60°,15°.
【解析】
(1)根据三角形的外角性质和对顶角的性质求出∠BED的度数;
(2)①由OD∥AB可得∠BOD=∠B=30°,再由∠BOD+∠BOC=90°和∠AOC+∠BOC=90°求出∠AOC的度数;②根据题意作图,可分6种情况进行分析求解.
(1)∵∠CEA=∠BAO-∠C=60°-45°=15°,
∴∠BED=∠CEA=15°,
(2)①∵OD∥AB,
∴∠BOD=∠B=30°
又∠BOD+∠BOC=90°和∠AOC+∠BOC=90°
∴∠AOC=∠BOD=30°;
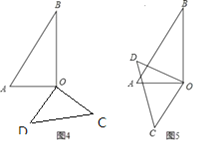
②存在,如图1,∵AB∥CO,
∴∠AOC=∠AOB+∠BOC=∠AOB+∠B=120°;
如图2,延长AO交CD于E,
∵AB∥DC,∴∠DEO=∠A=60°,又∠C=45°,∴∠COE=∠DEO-∠C=15°,
∴∠AOC=180°-∠COE=165°;
如图3,∵AB∥DO,
∴∠A+∠AOD=180°,
∵∠A=60°
∴∠AOD=120°
∴∠AOC=∠AOD-∠COD=30°;
如图4,∵AB∥DO,∴∠AOC=∠AOD+∠COD=∠BAO+∠COD=60°+90°=150°
如图5,∵AB∥CO,∴∠AOC=∠BAO =60°
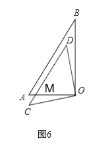
如图6,
设AO与CD相交于点M
∵AB∥CD,
∴∠DMO=∠A=60°
∴∠AOD=180°-45°-60°=75°,
∴∠AOC=90°-∠AOD =15°.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,将矩形ABCD沿对角线BD对折,使点C落在![]() 处,连接B
处,连接B![]() 交AD于点E,AB=4, BC=6.
交AD于点E,AB=4, BC=6.
求证: (1)AE=![]() E; (2)△EBD面积.
E; (2)△EBD面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m,n]上的“闭函数”.如函数y=﹣x+4,当x=1时,y=3;当x=3时,y=1,即当1≤x≤3时,恒有1≤y≤3,所以说函数y=﹣x+4是闭区间[1,3]上的“闭函数”,同理函数y=x也是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=![]() 是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2018]上的“闭函数”吗?请判断并说明理由;
(2)如果已知二次函数y=x2﹣4x+k是闭区间[2,t]上的“闭函数”,求k和t的值;
(3)如果(2)所述的二次函数的图象交y轴于C点,A为此二次函数图象的顶点,B为直线x=1上的一点,当△ABC为直角三角形时,写出点B的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
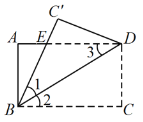
【题目】若将一幅三角板按如图所示的方式放置,则下列结论中不正确的是( )

A. ∠1=∠3 B. 如果∠2=30°,则有AC∥DE
C. 如果∠2=30°,则有BC∥AD D. 如果∠2=30°,必有∠4=∠C
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】按下面的程序计算:当输入x=100 时,输出结果是299;当输入x=50时,输出结果是446;如果输入 x 的值是正整数,输出结果是257,那么满足条件的x的值最多有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某路灯在铅垂面内的示意图,灯柱AC的高为11米,灯杆AB与灯柱AC的夹角∠A=120°,路灯采用锥形灯罩,在地面上的照射区域DE长为18米,从D,E两处测得路灯B的仰角分别为α和β,且tanα=6,tanβ=![]() ,求灯杆AB的长度.
,求灯杆AB的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,∠B=90°,AB∥CD,M为BC边上的一点,且AM平分∠BAD,DM平分∠ADC.

(1)求证:AM⊥DM;
(2)若BC=8,求点M到AD的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com