
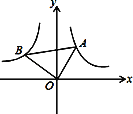
【题目】如图所示,点A在反比例函数![]() (x>0)的图象上,点B在反比例函数
(x>0)的图象上,点B在反比例函数![]() (x>0)的图象上,且∠AOB=90°,则tan∠OAB的值为_____.
(x>0)的图象上,且∠AOB=90°,则tan∠OAB的值为_____.
【答案】![]()
【解析】分析: 首先过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,易得△OBD∽△AOC,又由点A在反比例函数y=![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=![]() (x<0)的图象上,即可得S△OBD=4.5,S△AOC=2,然后根据相似三角形面积的比等于相似比的平方,即可得
(x<0)的图象上,即可得S△OBD=4.5,S△AOC=2,然后根据相似三角形面积的比等于相似比的平方,即可得![]() =
=![]() ,然后由正切函数的定义求得答案.
,然后由正切函数的定义求得答案.
详解: 过点A作AC⊥x轴于C,过点B作BD⊥x轴于D,
∴∠ACO=∠ODB=90°,
∴∠OBD+∠BOD=90°,
∵∠AOB=90°,
∴∠BOD+∠AOC=90°,
∴∠OBD=∠AOC,
∴△OBD∽△AOC,
∴![]() =(
=(![]() )2,
)2,
∵点A在反比例函数y=![]() (x>0)的图象上,点B在反比例函数y=
(x>0)的图象上,点B在反比例函数y=![]() (x<0)的图象上,
(x<0)的图象上,
∴S△OBD=4.5,S△AOC=2,
∴![]() =
=![]() ,
,
∴tan∠OAB=![]() =
=![]() .
.
故答案为:![]() .
.
点睛: 此题考查了相似三角形的判定与性质、反比例函数的性质以及直角三角形的性质.此题难度适中,注意掌握数形结合思想的应用,注意掌握辅助线的作法.


科目:初中数学 来源: 题型:
【题目】为了了解2014年某地区10万名大、中、小学生50米跑成绩情况,教育部门从这三类学生群体中各抽取了10%的学生进行检测,整理样本数据,并结合2010年抽样结果,得到下列统计图:
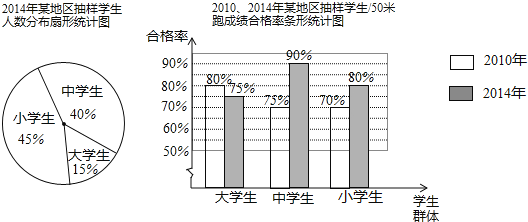
(1)本次检测抽取了大、中、小学生共 名,其中小学生 名;
(2)根据抽样的结果,估计2014年该地区10万名大、中、小学生中,50米跑成绩合格的中学生人数为 名;
(3)比较2010年与2014年抽样学生50米跑成绩合格率情况,写出一条正确的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
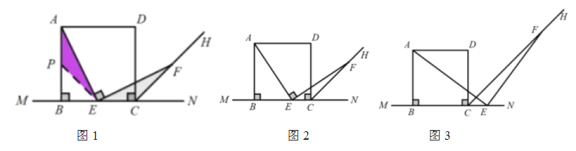
【题目】如图1,以直线MN上的线段BC为边作正方形ABCD,CH平分∠DCN,点E为射线BN上一点,连接AE,过点E作AE的垂线交射线CH于点F,探索AE与EF的数量关系。
(1)阅读下面的解答过程。并按此思路完成余下的证明过程
当点E在线段BC上,且点E为BC中点时,AB=EF
理由如下:
取AB中点P,達接PE
在正方形ABCD中,∠B=∠BCD=90°,AB=BC
∴△BPE等腰三角形,AP=BC
∴∠BPB=45°
∴∠APBE=135°
又因为CH平分∠DCN
∴∠DCF=45°
∴∠ECF=135°
∴∠APE=∠ECF
余下正明过程是:
(2)当点E为线段AB上任意一点时,如图2,结论“AE=EF”是否成立,如果成立,请给出证明过程;
(3)当点E在BC的延长线时,如图3,结论“AE=EF”是否仍然成立,如果成立,请在图3中画出必要的辅助线(不必说明理由)。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知
与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知![]() ,
,![]() .
.
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 在抛物线的对称轴上是否存在点P,使
在抛物线的对称轴上是否存在点P,使![]() 是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
![]() 点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,
点E时线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,![]() 的面积最大?求出
的面积最大?求出![]() 的最大面积及此时E点的坐标.
的最大面积及此时E点的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点![]() 为直线
为直线![]() 上一点,过点
上一点,过点![]() 作射线
作射线![]() ,使
,使![]() ,将一直角三角板的直角顶点放在点
,将一直角三角板的直角顶点放在点![]() 处,一边
处,一边![]() 在射线
在射线![]() 上,另一边
上,另一边![]() 在直线
在直线![]() 的上方.
的上方.
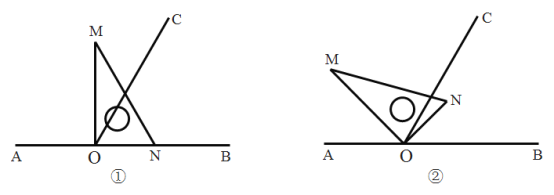
(1)在图①中,![]() __________度;
__________度;
(2)将图①中的三角板绕点![]() 按逆时针方向旋转,使得
按逆时针方向旋转,使得![]() 在
在![]() 的内部,如图②,若
的内部,如图②,若![]() ,求
,求![]() 的度数;
的度数;
(3)将图①中的三角板绕点![]() 以每秒
以每秒![]() 的速度沿逆时针方向旋转一周,在旋转的过程中,当直线
的速度沿逆时针方向旋转一周,在旋转的过程中,当直线![]() 恰好平分锐角
恰好平分锐角![]() 时,旋转的时间是__________秒.(直接写出结果)
时,旋转的时间是__________秒.(直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
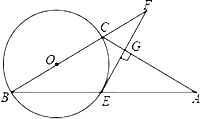
【题目】如图,已知△ABC中,AC=BC,以BC为直径的⊙O交AB于E,过点E作EG⊥AC于G,交BC的延长线于F.
(1)求证:FE是⊙O的切线;
(2)若FE=4,FC=2,求⊙O的半径及CG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将n个边长都为2的正方形按如图所示摆放,点A1,A2,…An分别是正方形的中心,则这n个正方形重叠部分的面积之和是( )

A.nB.n﹣1C.![]() D.
D.![]() n
n
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过点
经过点![]() ,
,![]() ,与
,与![]() 轴正半轴交于
轴正半轴交于![]() 点,与
点,与![]() 轴交于
轴交于![]() 点.
点.
(1)求直线![]() 的解析式;
的解析式;
(2)设点![]() 为直线
为直线![]() 下方抛物线上一点,连接
下方抛物线上一点,连接![]() 、
、![]() ,当
,当![]() 面积最大时,求点
面积最大时,求点![]() 的坐标;
的坐标;
(3)在(2)的条件下,直线![]() 过直线
过直线![]() 与
与![]() 轴的交点
轴的交点![]() .设
.设![]() 的中点为
的中点为![]() ,
,![]() 是直线
是直线![]() 上一点,
上一点,![]() 是直线
是直线![]() 上一点,求
上一点,求![]() 周长的最小值.
周长的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在数学活动课中,小敏为了测量校园内旗杆![]() 的高度.先在教学楼的底端
的高度.先在教学楼的底端![]() 点处,观测到旗杆顶端
点处,观测到旗杆顶端![]() 得
得![]() ,然后爬到教学楼上的
,然后爬到教学楼上的![]() 处,观测到旗杆底端
处,观测到旗杆底端![]() 的俯角是
的俯角是![]() .已知教学楼中
.已知教学楼中![]() 、
、![]() 两处高度为
两处高度为![]() 米.
米.
(1)求教学楼与旗杆的水平距离![]() ;(结果保留根号);
;(结果保留根号);
(2)求旗杆![]() 的高度.
的高度.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com