

分析 (1)根据题意得出BM,CN,易得BN,BA,分类讨论当△BMN∽△BAC时,利用相似三角形的性质得$\frac{BM}{BA}=\frac{BN}{BC}$,解得t;当△BMN∽△BCA时,$\frac{BM}{BC}=\frac{BN}{BA}$,解得t,综上所述,△BMN与△ABC相似,得t的值;
(2)过点M作MD⊥CB于点D,利用锐角三角函数易得DM,BD,由BM=3tcm,CN=2tcm,易得CD,利用三角形相似的判定定理得△CAN∽△DCM,由三角形相似的性质得$\frac{AC}{CN}=\frac{CD}{DM}$,解得t.
解答 解:(1)由题意知,BM=3tcm,CN=2tcm,
∴BN=(8-2t)cm,BA=$\sqrt{{6}^{2}+{8}^{2}}$=10(cm),
当△BMN∽△BAC时,$\frac{BM}{BA}=\frac{BN}{BC}$,
∴$\frac{3t}{10}=\frac{8-2t}{8}$,解得:t=$\frac{20}{11}$;
当△BMN∽△BCA时,$\frac{BM}{BC}=\frac{BN}{BA}$,
∴$\frac{3t}{8}=\frac{8-2t}{10}$,解得:t=$\frac{32}{23}$,
∴△BMN与△ABC相似时,t的值为$\frac{20}{11}$或$\frac{32}{23}$;
(2)过点M作MD⊥CB于点D,由题意得:
DM=BMsinB=3t$•\frac{6}{10}$=$\frac{9}{5}t$(cm),BD=BMcosB=3t$•\frac{8}{10}$=$\frac{12}{5}$t(cm),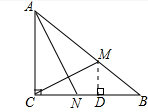
BM=3tcm,CN=2tcm,
∴CD=(8-$\frac{12}{5}t$)cm,
∵AN⊥CM,∠ACB=90°,
∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD,
∵MD⊥CB,
∴∠MDC=∠ACB=90°,
∴△CAN∽△DCM,
∴$\frac{AC}{CN}=\frac{CD}{DM}$,
∴$\frac{6}{2t}$=$\frac{8-\frac{12}{5}t}{\frac{9}{5}t}$,解得t=$\frac{13}{12}$或t=0(舍弃).
∴t=$\frac{13}{12}$.
点评 本题主要考查了动点问题,相似三角形的判定及性质等,分类讨论,数形结合是解答此题的关键.


 能考试期末冲刺卷系列答案
能考试期末冲刺卷系列答案科目:初中数学 来源: 题型:选择题

| A. | 147.40元 | B. | 143.17元 | C. | 144.23元 | D. | 136.83元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{2}$cm,3πcm2 | B. | 2$\sqrt{2}$cm,3πcm2 | C. | 2$\sqrt{2}$cm,6πcm2 | D. | $\sqrt{10}$cm,6πcm2 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
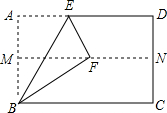 如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )
如图,在矩形ABCD中,M、N分别为边AB、CD的中点,将矩形ABCD沿BE折叠,使A点恰好落在MN上的点F处,则∠CBF的度数为( )| A. | 20° | B. | 25° | C. | 30° | D. | 36° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1的度数为( )
如图,含有30°的直角三角板△ABC,∠BAC=90°,∠C=30°,将△ABC绕着点A逆时针旋转,得到△AMN,使得点B落在BC边上的点M处,过点N的直线l∥BC,则∠1的度数为( )| A. | 15° | B. | 30° | C. | 45° | D. | 60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,AB=AC,BD⊥AC于点D,过点B作BE⊥BC交CA的延长线于点E,点P是BC的中点,连接PD,则下列结论:①∠BAC=2∠DBC;②BC2=2CD•AB;③若BC=15,BD=12,则AD=$\frac{7}{2}$;④图中一定相似的三角形有5对,其中正确结论的个数是( )
如图,在△ABC中,AB=AC,BD⊥AC于点D,过点B作BE⊥BC交CA的延长线于点E,点P是BC的中点,连接PD,则下列结论:①∠BAC=2∠DBC;②BC2=2CD•AB;③若BC=15,BD=12,则AD=$\frac{7}{2}$;④图中一定相似的三角形有5对,其中正确结论的个数是( )| A. | 2 | B. | 3 | C. | 1 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com