
【题目】利用完全平方公式因式分解在数学中的应用,请回答下列问题:
(1)因式分解:![]() _______.
_______.
(2)填空:
①当![]() 时,代数式
时,代数式![]() _______.
_______.
②当![]() _______时,代数式
_______时,代数式![]() ;
;
③代数式![]() 的最小值是_______.
的最小值是_______.
(3)拓展与应用:当![]() 、
、![]() 为何值时,代数式
为何值时,代数式![]() 有最小值,并求出这个最小值.
有最小值,并求出这个最小值.
【答案】(1)(x-2)2;(2)①0;②3;③-26;(3)a=2,b=4,最小值为10.
【解析】
(1)根据差的完全平方公式进行分解便可;
(2)①先分解因式,再代值计算;
②先对等式左边的代数式进行因式分解,再求未知数的值;
③通过因式分解把原式化成一个完全平方式与一个常数和的形式,便可求得最小值;
(3)利用完成完全平方式分解因式,把已知代数式转化为两个代数式的平方和与一个常数的和的形式,便可求得最小值.
(1)![]()
=x2-2×2x+22
=(x-2)2,
故答案为:(x-2)2;
(2)①![]()
=x2+2×2x+22
=(x+2)2
把x=-2代入上式得,
原式=(-2+2)2=0;
②![]() =(x-3)2=0,
=(x-3)2=0,
x-3=0,
x=3,
∴当x=3时,代数式x2-6x+9=0;
③![]() =x2-2×6x+62-26=(x-6)2-26,
=x2-2×6x+62-26=(x-6)2-26,
∵(x-6)2≥0,
∴(x-6)2-26≥-26,
∴代数式![]() 的最小值是-26,
的最小值是-26,
故答案为:①0;②3;③-26;
(3)![]() =(a-2)2+(b-4)2+10
=(a-2)2+(b-4)2+10
∵(a-2)2≥0,(b-4)2≥0
∴(a-2)2+(b-4)2+10≥10
∴当a=2,b=4时,代数式![]() 的最小值是10.
的最小值是10.


科目:初中数学 来源: 题型:
【题目】如图1,在数轴上点A,点B对应的数分别是6,﹣6,∠DCE=90°(点C与点O重合,点D在数轴的正半轴上)
(1)如图1,若CF平分∠ACE,则∠AOF= 度;点A与点B的距离=
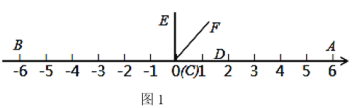
(2)如图2,将∠DCE沿数轴的正半轴向右平移t(0<t<3)个单位后,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α.

①当t=1时,α= ;点B与点C的距离=
②猜想∠BCE和α的数量关系,并说明理由;
(3)如图3,开始∠D1C1E1与∠DCE重合,将∠DCE沿数轴的正半轴向右平移t(0![]() t
t![]() 3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0
3)个单位,再绕点顶点C逆时针旋转30t度,作CF平分∠ACE,此时记∠DCF=α,与此同时,将∠D1C1E1沿数轴的负半轴向左平移t(0![]() t
t![]() 3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.
3)个单位,再绕点顶点C1顺时针旋转30t度,作C1F1平分∠AC1E1,记∠D1C1F1=β,若α与β满足|α﹣β|=20°,求t的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知如图,以Rt△ABC的AC边为直径作⊙O交斜边AB于点E,连接EO并延长交BC的延长线于点D,点F为BC的中点,连接EF.
(1)求证:EF是⊙O的切线;
(2)若⊙O的半径为3,∠EAC=60°,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算题 1、化简
2、若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
(1)先化简,再求值: ![]() ÷(2+
÷(2+ ![]() )
)
(2)若一次函数y=kx+b经过点A(3,4)、B(4,5),求这一次函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中点、平行线、等腰直角三角形、等边三角形都是常见的几何图形!
(1)如图1,若点D为等腰直角三角形ABC斜边BC的中点,点E,F分别在AB、AC边上,且∠EDF=90°,连接AD、EF,当BC=5 ![]() ,FC=2时,求EF的长度;
,FC=2时,求EF的长度;
(2)如图2,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;M为EF的中点,连接CM,当DF∥AB时,证明:3ED=2MC;
(3)如图3,若点D为等边三角形ABC边BC的中点,点E,F分别在AB,AC边上,且∠EDF=90°;当BE=6,CF=0.8时,直接写出EF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为( )

A.6B.8C.10D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
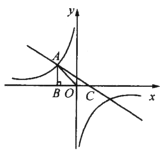
【题目】如图,已知反比例函数![]() (k<0)的图像经过点A(
(k<0)的图像经过点A(![]() ,m),过点A作AB⊥x轴于点,且△AOB的面积为
,m),过点A作AB⊥x轴于点,且△AOB的面积为![]() .
.
(1)求k和m的值;
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点C,求∠ACO的度数及![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com