
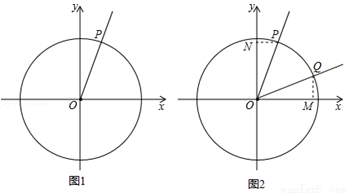
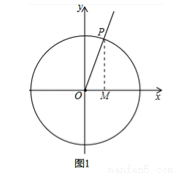
(本题满分12分)定义:如图1,射线OP与原点为圆心,半径为1的圆交于点P,记∠xOP=α,则点P的横坐标叫做角 的余弦值,记作
的余弦值,记作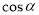 ;点P的纵坐标叫做角
;点P的纵坐标叫做角 的正弦值,记作
的正弦值,记作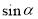 ;纵坐标与横坐标的比值叫做角
;纵坐标与横坐标的比值叫做角 的正切值,记作
的正切值,记作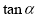 .
.
如:当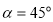 时, 点P的横坐标为
时, 点P的横坐标为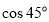 =
=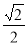 ,纵坐标为
,纵坐标为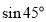 =
=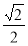 即P(
即P(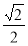 ,
,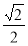 ).
).
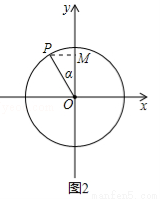
又如:在图2中,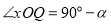 (
( 为锐角), PN
为锐角), PN
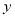 轴,QM
轴,QM
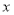 轴,易证△OQM≌△OPN, 则Q点的纵坐标
轴,易证△OQM≌△OPN, 则Q点的纵坐标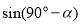 等于点P的横坐标
等于点P的横坐标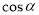 ,得
,得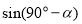 =
= 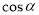 .
.
解决以下四个问题:
(1)当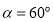 时,求点P的坐标;
时,求点P的坐标;
(2)当 是锐角时,则
是锐角时,则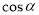 +
+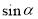 1(用>或<填空),
1(用>或<填空),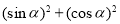 = ;
= ;
(3)求证: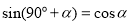 (
( 为锐角);
为锐角);
(4)求证:tan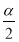 =
=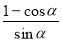 (
( 为锐角);
为锐角);
(1)(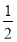 ,
,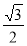 );(2)
);(2) >,1;(3)证明见试题解析;(4)证明见试题解析.
>,1;(3)证明见试题解析;(4)证明见试题解析.
【解析】
试题分析:(1)点P的横坐标为cos60°,纵坐标为sin60°,从而可得点P的坐标;
(2)结合图形可在△POM中,表示出cosα+sinα,继而与半径长1,比较即可;根据勾股定理可得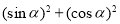 =1;
=1;
(3)画出图形,根据cosα及sin(90°+α)表示的实际意义,可得出结论;
(4)构造图形,如图,分别表示出tan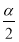 ,及
,及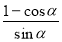 表示的线段比,继而可得出结论.
表示的线段比,继而可得出结论.
试题解析:(1)点P的坐标为(cos60°,sin60°)=(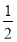 ,
,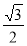 );
);
(2)如图1所示:∠MOP=α,∵半径为1,∴cosα=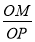 =OM,sinα=
=OM,sinα=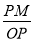 =PM,
=PM,
∴cosα+sinα=OM+PM>OP=1;
∴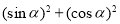 =
=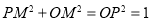 ;
;
(3)如图2所示:∠MOP=α,点P的纵坐标为sin(90°+α),值为OM的长度,cosα=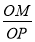 =OM,∴sin(90°+α)=cosα;
=OM,∴sin(90°+α)=cosα;
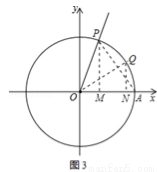
(4)如图3所示:∠AOQ=∠POQ=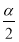 ,∠AOP=α,则cosα=
,∠AOP=α,则cosα=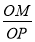 =OM,sinα=
=OM,sinα=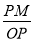 =PM,∴
=PM,∴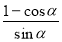 =
=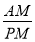 =tan∠APM,∵OQ是∠AOP的角平分线,∴OQ⊥AP,∴∠AOQ+∠OAP=90°,∵∠APM+∠OAP=90°,∴∠AOP=∠APM,即
=tan∠APM,∵OQ是∠AOP的角平分线,∴OQ⊥AP,∴∠AOQ+∠OAP=90°,∵∠APM+∠OAP=90°,∴∠AOP=∠APM,即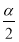 =∠APM,∴tan
=∠APM,∴tan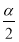 = tan∠APM =
= tan∠APM =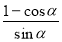 .
.
考点:圆的综合题.


科目:初中数学 来源:2014-2015学年内蒙古赤峰市宁城县七年级上学期期末考试数学试卷(解析版) 题型:填空题
在-5,-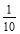 ,-3.5,-0.01,-2,-212各数中,最大的数是 .
,-3.5,-0.01,-2,-212各数中,最大的数是 .
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:解答题
已知二次函数y=x2﹣4x+3.
(1)用配方法求其图象的顶点C的坐标,并描述该函数的函数值随自变量的增减而变化的情况;
(2)求函数图象与x轴的交点A,B的坐标,及△ABC的面积.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:选择题
如图是二次函数y=ax2+bx+c的图象的一部分,对称轴是直线x=1.
①b2>4ac;
②4a﹣2b+c<0;
③不等式ax2+bx+c>0的解集是x≥3.5;
④若(﹣2,y1),(5,y2)是抛物线上的两点,则y1<y2.
上述4个判断中,正确的是( )
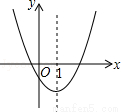
A. ①② B. ①④ C. ①③④ D. ②③④
查看答案和解析>>
科目:初中数学 来源:2014-2015学年山东省九年级上学期12月月考数学试卷(解析版) 题型:选择题
对于二次函数y=(x﹣1)2+2的图象,下列说法正确的是( )
A.开口向 下 B.对称轴是x=﹣1
C.顶点坐标是(1,2)D.与x轴有两个交点
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省射阳县九年级上学期期末考试数学试卷(解析版) 题型:解答题
(本题满分8分)在平面直角坐标系xOy中,直线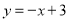 与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数1、2、3、
与两坐标轴围成一个△AOB.现将背面完全相同,正面分别标有数1、2、3、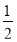 、
、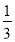 的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,再在剩下的4张卡片中任取一张,将该卡片上的数作为点P的纵坐标,请用所学的知识求出点P落在△AOB内部(不包括边界)的概率.
的5张卡片洗匀后,背面朝上,从中任取一张,将该卡片上的数作为点P的横坐标,再在剩下的4张卡片中任取一张,将该卡片上的数作为点P的纵坐标,请用所学的知识求出点P落在△AOB内部(不包括边界)的概率.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省射阳县九年级上学期期末考试数学试卷(解析版) 题型:填空题
一山坡的的坡比为3:4,一人沿山坡向上走了20米,那么这人垂直高度上升了_ _米.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省东台市九年级上学期第二次月考数学试卷(解析版) 题型:解答题
(本题满分10分)沿海开发公司准备投资开发A、B两种新产品,通过市场调研发现:
(1)若单独投资A种产品,则所获利润yA(万元)与投资金额x(万元)之间满足正比例函数关系:yA=kx;
(2)若单独投资B种产品,则所获利润yB(万元)与投资金额x(万元)之间满足二次函数关系:yB=ax2+bx.
(3)根据公司信息部的报告,yA,yB(万元)与投资金额x(万元)的部分对应值如下表所示:

(1)填空:yA= ;yB= ;
(2)若公司准备投资20万元同时开发A、B两种新产品,设公司所获得的总利润为W(万元),试写出W与某种产品的投资金额x(万元)之间的函数关系式;
(3)请你设计一个在(2)中能获得最大利润的投资方案,并求出按此方案能获得的最大利润是多少万元?
查看答案和解析>>
科目:初中数学 来源:2014-2015学年湖南省娄底市九年级上学期期末模拟考试数学试卷(解析版) 题型:选择题
某种药品原价为36元/盒.经过连续两次降价后售价为25元/盒.设平均每次降价的百分率为x,根据题意所列方程正确的是( )
A.36(1-x)2=36-25 B.36 (1-2x) =25
C.36(1-x)2=25 D.36(1-x2)=25
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com