
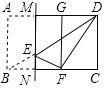
【题目】如图,在矩形ABCD中,AB:BC=3:5,点E是对角线BD上一动点(不与点B,D重合),将矩形沿过点E的直线MN折叠,使得点A,B的对应点G,F分别在直线AD与BC上,当△DEF为直角三角形时,CN:BN的值为______.
【答案】![]() 或
或![]()
【解析】
因为点A,B的对应点G,F分别在直线AD与BC上,所以分两种情况讨论, 当∠EFD=90°时,证明△EFN∽△FDC,设CD=5a,根据比例式表示出CN,BN即可;当∠EDF=90°时,证明△FCD∽△DCB,设CD=3a, 根据比例式表示出CN,BN即可.
解:分两种情况:
当∠EFD=90°时,如下图,
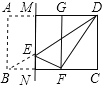
∵∠EFN=∠C=90°,易证∠EFN=∠FDC,
∴△EFN∽△FDC,
设CD=5a,由题可知,CF=3a,
∴![]() ,∴BC=
,∴BC=![]() ,
,
∴BN=NF=![]() ,即
,即![]()
当∠EDF=90°时,如下图,
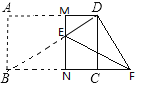
同理易证:△FCD∽△DCB,
设CD=3a,则BC=5a,CF=![]()
∴BF=5a+![]() ,
,
∴BN=![]() ,NC=
,NC=![]() ,
,
∴![]()
综上, CN:BN的值为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
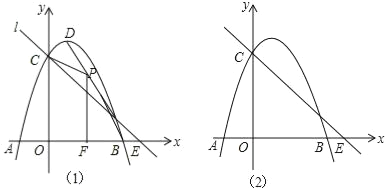
【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小红同学用仪器测量一棵大树AB的高度,在C处测得∠ADG=30°,在E处测得∠AFG=60°,CE=8米,仪器高度CD=1.5米,求这棵树AB的高度(结果保留两位有效数字,![]() ≈1.732).
≈1.732).
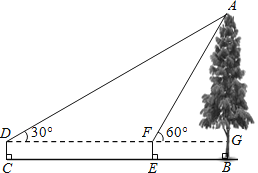
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+2与抛物线y=ax2+bx+6(a≠0)相交于A(![]() )和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
)和B(4,m),点P是线段AB上异于A、B的动点,过点P作PC⊥x轴于点D,交抛物线于点C.
(1)B点坐标为 ,并求抛物线的解析式;
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,直接写出此时点P的坐标.
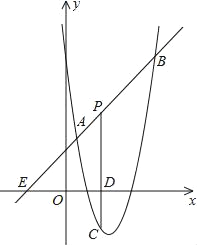
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在矩形纸片ABCD中,AB=4,AD=12,将矩形纸片折叠,使点C落在AD边上的点M处,折痕为PE,此时PD=3.
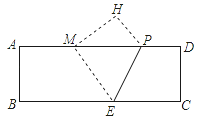
(1)求MP的值;
(2)在AB边上有一个动点F,且不与点A,B重合.当AF等于多少时,△MEF的周长最小?
(3)若点G,Q是AB边上的两个动点,且不与点A,B重合,GQ=2.当四边形MEQG的周长最小时,求最小周长值.(计算结果保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对任意一个四位数n,如果千位与十位上的数字之和为9,百位与个位上的数字之和也为9,则称n为“极数”,记为n=![]() 其中
其中![]() ,且x、y为整数
,且x、y为整数![]()
![]() 请任意写出两个“极数”;
请任意写出两个“极数”;
![]() 猜想任意一个“极数”是否是99的倍数,请说明理由;
猜想任意一个“极数”是否是99的倍数,请说明理由;
![]() 如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数,若四位数m为“极数”,记
如果一个正整数a是另一个正整数b的平方,则称正整数a是完全平方数,若四位数m为“极数”,记![]() 写出三个满足
写出三个满足![]() 是完全平方数的
是完全平方数的![]() 只需直接写出结果
只需直接写出结果![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰△OBC的边OB在x轴上,OB=CB,OB边上的高CA与OC边上的高BE相交于点D,连接OD,AB=![]() ,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
,∠CBO=45°,在直线BE上求点M,使△BMC与△ODC相似,则点M的坐标是________.
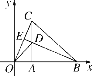
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列方程,①3x2+x=20,②2x2-3xy+4=0,③![]() ,④x2=0,⑤x2-3x-4=0.是一元二次方程的是( )
,④x2=0,⑤x2-3x-4=0.是一元二次方程的是( )
A. ①②B. ①②④⑤C. ①③④D. ①④⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com