
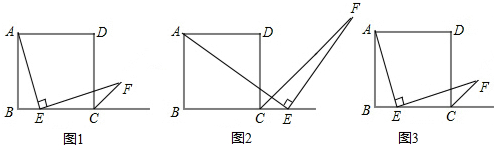
分析 (1)取AB的中点H,连接EH,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;
(2)成立,延长BA到M,使AM=CE,根据已知及正方形的性质利用ASA判定△AHE≌△ECF,从而得到AE=EF;
(3)存在,作DM⊥AE于AB交于点M,则有:DM∥EF,连接ME、DF,证明△ADM≌△BAE(ASA),得到DM=AE,由(1)AE=EP,所以DM=EP,所以四边形DMEP为平行四边形.
解答 (1)证明:取AB的中点H,连接EH;如图1所示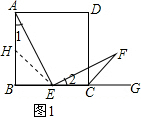
∵四边形ABCD是正方形,AE⊥EF;
∴∠1+∠AEB=90°,∠2+∠AEB=90°
∴∠1=∠2,
∵BH=BE,∠BHE=45°,且∠FCG=45°,
∴∠AHE=∠ECF=135°,AH=CE,在△AHE和△ECF中,$\left\{\begin{array}{l}{∠1=∠2}&{\;}\\{AH=CE}&{\;}\\{∠AHE=∠ECF}&{\;}\end{array}\right.$,
∴△AHE≌△ECF(ASA),
∴AE=EF;
(2)解:AE=EF成立,
理由如下:如图2,延长BA到M,使AM=CE,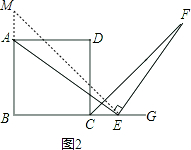
∵∠AEF=90°,
∴∠FEG+∠AEB=90°.
∵∠BAE+∠AEB=90°,
∴∠BAE=∠FEG,
∴∠MAE=∠CEF.
∵AB=BC,
∴AB+AM=BC+CE,
即BM=BE.
∴∠M=45°,
∴∠M=∠FCE.
$\left\{\begin{array}{l}{∠MAE=∠CEF}\\{AM=CE}\\{∠M=∠FCE}\end{array}\right.$,
∴△AME≌△ECF(ASA),
∴AE=EF.
(3)存在,
理由如下:如图3,作DM⊥AE于AB交于点M,则有:DM∥EF,连接ME、DF,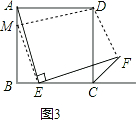
在△ADM与△BAE中,$\left\{\begin{array}{l}{∠ADM=∠BAE}&{\;}\\{AD=AB}&{\;}\\{∠DAM=∠ABE}&{\;}\end{array}\right.$,
∴△ADM≌△BAE(ASA),
∴DM=AE,
∵由(1)AE=EP,
∴DM=EP,
∴四边形DMEP为平行四边形.
点评 此题考查学生对正方形的性质及全等三角形判定的理解及运用,解决本题的关键是作出辅助线.


 小夫子全能检测系列答案
小夫子全能检测系列答案科目:初中数学 来源: 题型:解答题
 如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1,n)两点.
如图,一次函数y=kx+b的图象与反比例函数y=$\frac{m}{x}$的图象相交于A(-2,1)、B(1,n)两点.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
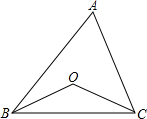 如图所示,在△ABC中,BO、CO是角平分线.
如图所示,在△ABC中,BO、CO是角平分线.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
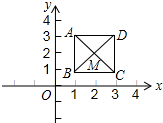 如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为(-2013,-2).
如图,已知正方形ABCD,顶点A(1,3)、B(1,1)、C(3,1).规定“把正方形ABCD先沿x轴翻折,再向左平移1个单位”为一次变换,如此这样,连续经过2015次变换后,正方形ABCD的对角线交点M的坐标变为(-2013,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
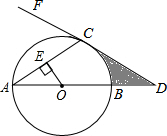 已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.
已知:在⊙O中,AB是直径,AC是弦,OE⊥AC于点E,过点C作直线FC,使∠FCA=∠AOE,交AB的延长线于点D.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
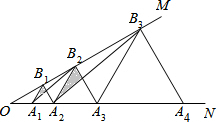 如图,已知∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,分别连接A1B2,连接A2B3….若OA1=a,从左往右的阴影面积依次记作S1、S2、S3…Sn.则Sn=$\frac{{4}^{n-2}\sqrt{3}{a}^{2}}{3}$.
如图,已知∠MON=30°,点A1、A2、A3在射线ON上,点B1、B2、B3…在射线OM上,△A1B1A2、△A2B2A3、△A3B3A4…均为等边三角形,分别连接A1B2,连接A2B3….若OA1=a,从左往右的阴影面积依次记作S1、S2、S3…Sn.则Sn=$\frac{{4}^{n-2}\sqrt{3}{a}^{2}}{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com