
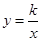 (x>0)的图像经过点A,若S△BEC=8,则k等于( ).
(x>0)的图像经过点A,若S△BEC=8,则k等于( ).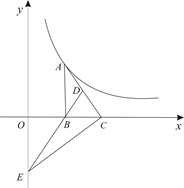
| A.16 | B.12 |
| C.8 | D.4 |

 ,
, AB=
AB= ,
, ,BC=2y,
,BC=2y, BC?E=
BC?E= ?
? ?2y=
?2y=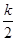 =8,
=8, =
= ,
, ×BC?OE=8,
×BC?OE=8,

科目:初中数学 来源:不详 题型:解答题
 (
(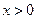 )的图象与一次函数
)的图象与一次函数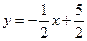 的图象交于
的图象交于 两点,点
两点,点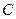 的坐标为
的坐标为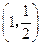 ,连接
,连接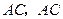 平行于
平行于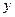 轴.
轴.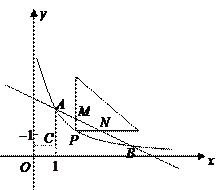
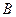 的坐标.
的坐标.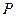 在反比例函数图象上的
在反比例函数图象上的 之间的部分滑动(不与
之间的部分滑动(不与 重合),两直角边始终分别平行于
重合),两直角边始终分别平行于 轴、
轴、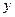 轴,且与线段
轴,且与线段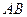 交于
交于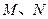 两点,试判断
两点,试判断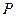 点在滑动过程中
点在滑动过程中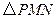 是否与
是否与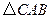 总相似,简要说明判断理由.
总相似,简要说明判断理由.查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
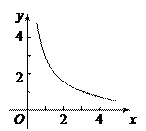 (3)在这个函数图象的某一支上任取点A(a1,b1)和点B(a2,b2),如果a1<a2,试比较b1和b2的大小.
(3)在这个函数图象的某一支上任取点A(a1,b1)和点B(a2,b2),如果a1<a2,试比较b1和b2的大小.查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
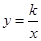 的图像经过点B,则
的图像经过点B,则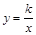
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com