
����Ŀ����ͼ�����κ���![]() ��
��![]() ����ͼ����
����ͼ����![]() �ύ��
�ύ��![]() ���㣬��
���㣬��![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() ������
������![]() ���������ֱ�Ϊ
���������ֱ�Ϊ![]() ��
��![]() ���ҵ�
���ҵ�![]() ��
��![]() ʱ���κ����ĺ���ֵ
ʱ���κ����ĺ���ֵ![]() ��ȣ�
��ȣ�
��1����ʵ��![]() ��ֵ��
��ֵ��
��2������![]() ͬʱ��
ͬʱ��![]() �����������ÿ��1����λ���ȵ��ٶȷֱ���
�����������ÿ��1����λ���ȵ��ٶȷֱ���![]() ���˶�������һ���㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ
���˶�������һ���㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶������˶�ʱ��Ϊ![]() ��ʱ������
��ʱ������![]() ����
����![]() ��
��![]() ���ۣ�
���ۣ�![]() ��ǡ������
��ǡ������![]() ���ϵ�
���ϵ�![]() ������
������![]() ��ֵ����
��ֵ����![]() �����ꣻ
�����ꣻ
��3���ڣ�2���������£����κ���ͼ��ĶԳ������Ƿ���ڵ�![]() ��ʹ����
��ʹ����![]() Ϊ������������
Ϊ������������![]() ���ƣ�������ڣ��������
���ƣ�������ڣ��������![]() �����ꣻ��������ڣ���˵�����ɣ�
�����ꣻ��������ڣ���˵�����ɣ�
���𰸡���1��![]() ����2��t=
����2��t=![]() ��
�� 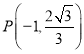 ����3��Q��-1��
����3��Q��-1��![]() ����������.
����������.
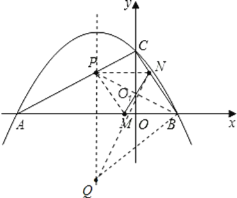
��������
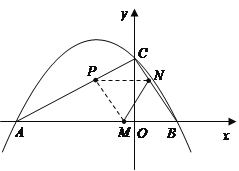
��1���������ͼ�ο���������ı���ʽ��
��2������������ڲ����ι�ϵ���������tֵ��P�����ꣻ
��3�����������1��������ACB�ס�QNB���С�ABC=��QBN��Ѱ�������������ж��Ƿ����㣮
�⣺��1����![]() ����������
����������
������c=![]()
��x=-4��x=2ʱ���κ����ĺ���ֵy��ȣ�
�ඥ�������![]() ,
,
![]() ,
,
�֡�A��-3��0�����������ϣ�
��9a3b+![]() =0
=0
�����϶�ʽ��![]() ;
;
��2���ɣ�1��![]() ,
,
��B��1��0����
����BP��MN�ڵ�O1�������۵������ʿɵã�O1ҲΪPB�е㣮
��t�����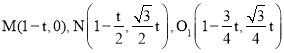 ,
,
��P��x��y����B��1��0��
��O1ΪP��B���е�ɵ�![]() ����
����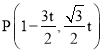 ,
,
��A��C������֪AC��![]() ��P��Ҳ��ֱ��AC�ϴ����t=
��P��Ҳ��ֱ��AC�ϴ����t=![]() ,
,
��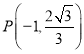 ��
��
��3�����������
��������ACB�ס�QNB�����С�ABC=��QBN��
��Q����x���ϣ�AC��QN��������A��C��Q��N����ֱ֪�ߵ�һ����ϵ��Ϊ��![]() ��
��
����ACB������QNB���ƣ�
��������ACB�ס�QBN������![]()
��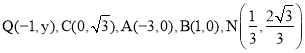 ��
��
��![]() ��
��
���루1����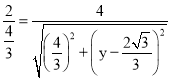 ��
��
![]() ��
��![]() ��
��
��![]() ʱ��Q��-1��
ʱ��Q��-1��![]() ����
����![]() ������������ȥ��
������������ȥ��
��y=![]() ��Q��-1��
��Q��-1��![]() ����
����![]() ��
��
����ڵ�Q��-1��![]() ��ʹ��ACB�ס�QBN��
��ʹ��ACB�ס�QBN��
���Ͽɵã�Q��-1��![]() ��.
��.


 ���ƽ̸�������ѡ����ĩ���100��ϵ�д�
���ƽ̸�������ѡ����ĩ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���廧����һ��ʱ��ˮ����20��������ϣ���������������������˸��ټ�¼����������¼�����ݿɻ�����ͼ��ʾ�ĺ���ͼ��������������y��ǧ�ˣ�������ʱ��x���죩֮��ĺ�����ϵ��ͼ��ʾ��������˵������ȷ���ǣ� ��

A.��10������20ǧ��B.һ���������30ǧ��
C.��9�����16�������������ͬD.��19��ȵ�1�������4ǧ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��λ�蹺��ס������������������˽⣬�������������ļ۸������ۼۺ�������(���������ۣ���ÿ�����������������������50Ͱ)������ʱ����������ÿͰ��������������8Ԫ����֪����������������![]() (
(![]() )Ͱ��������÷ֱ���960Ԫ��720Ԫ��
)Ͱ��������÷ֱ���960Ԫ��720Ԫ��
��1����ס������������������ۼۣ�
��2���õ�λԤ������������������500Ͱ���Ҽ�������������������������������������![]() ���ס��������������������۷ֱ�Ϊ20Ԫ/Ͱ��16Ԫ/Ͱ���������������������Ϊ
���ס��������������������۷ֱ�Ϊ20Ԫ/Ͱ��16Ԫ/Ͱ���������������������Ϊ![]() Ͱ�������ʽ��ܶ�Ϊ
Ͱ�������ʽ��ܶ�Ϊ![]() (Ԫ)����д��
(Ԫ)����д��![]() ��
��![]() �ĺ�����ϵʽ�������
�ĺ�����ϵʽ�������![]() ����Сֵ�ʹ�ʱ�Ĺ�����
����Сֵ�ʹ�ʱ�Ĺ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������κ���y=ax2+bx+c��ͼ����x�������������㣬��ôһԪ���η���ax2+bx+c=0����������ȵ�ʵ������������������仰�����⣬����������⣺��m��n��m��n���ǹ���x�ķ���1����x��a����x��b��=0����������a��b����a��b��m��n�Ĵ�С��ϵ�ǣ� ����
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij���˻��ڿ���![]() ��̽�Ŀ��
��̽�Ŀ��![]() �ĸ��Ƿֱ���
�ĸ��Ƿֱ���![]() ,��ʱ���˻��ķ��и߶�
,��ʱ���˻��ķ��и߶�![]() Ϊ
Ϊ![]() ��������˻���
��������˻���![]() ������ˮƽ����
������ˮƽ����![]() m����
m����![]() ��.
��.
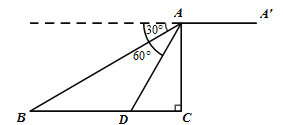
��1����![]() ֮��ľ���
֮��ľ���
��2��������˻�![]() �Ͽ�Ŀ��
�Ͽ�Ŀ��![]() �ĸ��ǵ�����ֵ.
�ĸ��ǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������С������12�֣�
��֪����Rt��ABC��Rt��DEF����ͼ��1���ڷţ���C���E�غϣ�����B��C��E����F��ͬһ��ֱ���ϣ���ACB = ��EDF = 90�㣬��DEF = 45����AC = 8 cm��BC = 6 cm��EF = 9 cm��
��ͼ��2������DEF��ͼ��1����λ�ó�������1 cm/s���ٶ���CB����ABC��������������DEF������ͬʱ����P����ABC�Ķ���B��������2 cm/s���ٶ���BA���A��������.����DEF�Ķ���D�ƶ���AC����ʱ����DEFֹͣ��������PҲ��ֹ֮ͣ�ƶ���DE��AC�ཻ�ڵ�Q������PQ��������ʱ��Ϊt��s����0��t��4.5����

����������⣺
��1����tΪ��ֵʱ����A���߶�PQ�Ĵ�ֱƽ�����ϣ�
��2������PE�����ı���APEC�����Ϊy��cm2������y��t֮��ĺ�����ϵʽ���Ƿ����ijһʱ��t��ʹ���y��С�������ڣ����y����Сֵ���������ڣ�˵�����ɣ�
��3���Ƿ����ijһʱ��t��ʹP��Q��F������ͬһ��ֱ���ϣ������ڣ������ʱt��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijѧУ��չ�˷���֪ʶ�������������Ϊ�˽���λ��Ч����ѧУ��ȫУ1500��ѧ���������ȡ����ѧ������֪ʶ���ԣ���������100�֣��÷�x��Ϊ��С��60�����������������Գɼ���Ϊ�ĸ��ȵڣ������ϸ�60��x��70�����ϸ�70��x��80�������ã�80��x��90�������㣨90��x��100������������ͼͳ��ͼ��������Ϣδ��������
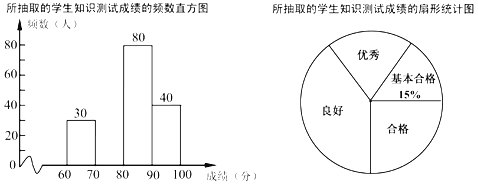
��ͼ�и�������Ϣ����������⣺
��1������Գɼ�Ϊ�ϸ��ѧ������������ȫƵ��ֱ��ͼ��
��2��������ͳ��ͼ�С����á�����Ӧ������Բ�ĽǵĶ�����
��3����β��Գɼ�����λ����ʲô�ȵڣ�
��4�����ȫУѧ�����μӲ��ԣ�������ݳ������ԵĽ�������Ƹ�У��������ѧ���ж����ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ˮ��ɽ���ǽ�ɽ��ɽ�����ҳ���ȫ��ֲ�����ڽ���3��12��ֲ���ڵ��죬ijУ���꼶һ��48��ѧ��ȫ���μ���ֲ���������ÿ������4�꣬Ů��ÿ������3�꣬ȫ�����170�ꡣ
��1���ð��С�Ů����Ϊ�����ˣ�
��2��ѧУѡ����ס����������磬������![]() ��������
��������![]() .���Ҫʹ���������Ǯ������1200Ԫ����ô�����Թ������������ꣿ
.���Ҫʹ���������Ǯ������1200Ԫ����ô�����Թ������������ꣿ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�İ뾶Ϊ6cm��BΪ��O��һ�㣬OB����O�ڵ�A��AB=OA������P�ӵ�A���������� cm/s���ٶ�����O�ϰ���ʱ�뷽���˶�һ�ܻص���A����ֹͣ������P�˶���ʱ��Ϊ______ʱ��BP����O���У�
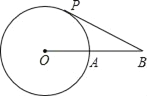
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com