
分析 (1)根据判别式的意义得到△=42-4(m-1)>0,然后解不等式即可;
(2)在(1)的范围内取m=1,则根据根与系数的关系得到x1+x2=-4,x1x2=0,再把x${\;}_{1}^{2}$+x${\;}_{2}^{2}$+x1x2变形为(x1+x2)2-x1x2,然后利用整体代入的方法计算.
解答 解:(1)根据题意得△=42-4(m-1)>0,
解得m<5;
(2)当m=1时,方程化为x2+4x=0,
则x1+x2=-4,x1x2=0,
所以x${\;}_{1}^{2}$+x${\;}_{2}^{2}$+x1x2=(x1+x2)2-x1x2=(-4)2-0=16.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:解答题
| 年份 品种 | 2014年 | 2015年 |
| 平均每亩产量(kg) | 300 | 300(1+x) |
| 养殖面积(亩) | 20 | 20(1+2x) |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5,7 | B. | 7,5 | C. | 4,7 | D. | 3,7 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
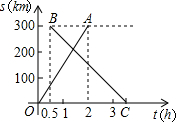 在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题:
在甲、乙两城市之间每隔1小时有一列速度相同的动车组列车从甲城开往乙城.如图所示,OA是第一列动车组列车离开甲城的路程s(千米)与运行时间t(时)的函数图象,BC是一列从乙城开往甲城的普通快车距甲城的路程s(千米)与运行时间t(时)的函数图象.请根据图中信息,解答下列问题:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com