
分析 点A向上平移2个单位到M,点B关于y轴的对称点B′,连接MB′,交y轴于C,要使得四边形ABCD的周长最短,只要BC+AD最小就行.
解答 解:∵A(-4,0),B(-4,4),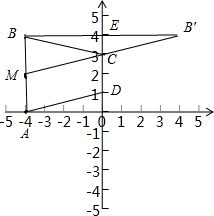
∴AB=4,
又∵C、D在y轴上,点C在点D上方,CD=2.
∴要使得四边形ABCD的周长最短,只要BC+AD最小即可,
点A向上平移2个单位到M,点B关于y轴的对称点B′,连接MB′,交y轴于C,
∵BM=2,
∴CE=1,
∴OC=3,
∴C(0,3)
故答案为:(0,3).
点评 本题考查了矩形的性质,平面直角坐标系上点的坐标,轴对称-最短路线问题的应用,题目具有一定的代表性,但是一道难度偏大的题目,对学生提出较高的要求.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
 如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )
如图,以G(0,1)为圆心,2为半径的圆与x轴交于A、B两点,与y轴交于C、D两点,点E为圆G上一动点,CF⊥AE于F,当点E从点B出发顺时针运动到点D时,点F经过的路径长为( )| A. | $\frac{{\sqrt{3}}}{2}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{{\sqrt{3}}}{4}$ | D. | $\frac{{\sqrt{3}}}{6}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 事件A发生的频率是$\frac{7}{100}$ | |
| B. | 反复大量做这种试验,事件A只发生了7次 | |
| C. | 做100次这种试验,事件A一定发生7次 | |
| D. | 做100次这种试验,事件A可能发生7次 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
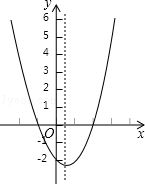 二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )
二次函数y=ax2+bx+c(a≠0)的大致图象如图,关于该二次函数,下列说法错误的是( )| A. | 函数有最小值 | B. | 对称轴是直线x=$\frac{1}{2}$ | ||
| C. | 当-1<x<2时,y>0 | D. | 当x<$\frac{1}{2}$,y随x的增大而减小 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
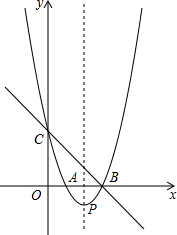 如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.
如图(1),直线y=-x+3与x轴、y轴分别交于点B、点C,经过B、C两点的抛物线y=x2+bx+c与x轴的另一个交点为A,顶点为P.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com