
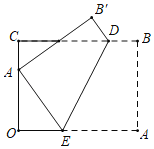
【题目】如图,矩形OABC中,OA=4,AB=3,点D在边BC上,且CD=3DB,点E是边OA上一点,连接DE,将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,则OE的长为( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
【答案】B
【解析】
连接A′D,AD,根据矩形的性质得到BC=OA=4,OC=AB=3,∠C=∠B=∠O=90°,求得CD=3,BD=1,根据折叠的得到A′D=AD,A′E=AE,根据全等三角形的性质得到A′C=BD=1,根据勾股定理即可得到结论.
解:连接A′D,AD,
∵四边形OABC是矩形,
∴BC=OA=4,OC=AB=3,∠C=∠B=∠O=90°,
∵CD=3DB,
∴CD=3,BD=1,
∴CD=AB,
∵将四边形ABDE沿DE折叠,若点A的对称点A′恰好落在边OC上,
∴A′D=AD,A′E=AE,
在Rt△A′CD与Rt△DBA中,![]() ,
,
∴Rt△A′CD≌Rt△DBA(HL),
∴A′C=BD=1,
∴A′O=2,
∵A′O2+OE2=A′E2,
∴22+OE2=(4﹣OE)2,
∴![]()
故选:B.



 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源: 题型:
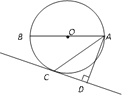
【题目】如图,已知AB是⊙O的直径,AC为弦,且平分∠BAD,AD⊥CD,垂足为D.
(1) 求证:CD是⊙O的切线;
(2) 若⊙O的直径为4,AD=3,试求∠BAC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场以每件20元购进一批衬衫,若以每件40元出售,则每天可售出60件,经调查发现,如果每件衬衫每涨价1元,商场平均每天可少售出2件,若设每件衬衫涨价![]() 元,回答下列问题:
元,回答下列问题:
(1)该商场每天售出衬衫 件(用含![]() 的代数式表示);
的代数式表示);
(2)求![]() 的值为多少时,商场平均每天获利1050元?
的值为多少时,商场平均每天获利1050元?
(3)该商场平均每天获利 (填“能”或“不能”)达到1250元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,直线y=x+4与y=kx+4分别交x轴于点A、B,两直线交于y轴上同一点C,点D的坐标为(﹣![]() ,0),点E是AC的中点,连接OE交CD于点F.
,0),点E是AC的中点,连接OE交CD于点F.

(1)求点F的坐标;
(2)若∠OCB=∠ACD,求k的值;
(3)在(2)的条件下,过点F作x轴的垂线1,点M是直线BC上的动点,点N是x轴上的动点,点P是直线l上的动点,使得以B,P,M、N为顶点的四边形是菱形,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小元设计的“过圆上一点作圆的切线”的尺规作图过程.
已知:如图,⊙O及⊙O上一点P.
求作:过点P的⊙O的切线.


作法:如图,
①作射线OP;
②在直线OP外任取一点A,以点A为圆心,AP为半径作⊙A,与射线OP交于另一点B;
③连接并延长BA与⊙A交于点C;
④作直线PC;
则直线PC即为所求.
根据小元设计的尺规作图过程,
(1)使用直尺和圆规,补全图形;(保留作图痕迹)
(2)完成下面的证明:
证明:∵ BC是⊙A的直径,
∴∠BPC=90°(____________)(填推理的依据).
∴OP⊥PC.
又∵OP是⊙O的半径,
∴PC是⊙O的切线(____________)(填推理的依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
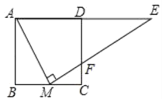
【题目】如图,正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于点F,交AD的延长线于点E,若AB=4,BM=2,则△DEF的面积为( )
A.9B.8C.15D.14.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正比例函数y=x的图象与反比例函数y=![]() (k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(k为常数,且k≠0)的图象有一个交点的纵坐标是2.
(Ⅰ)当x=4时,求反比例函数y=![]() 的值;
的值;
(Ⅱ)当﹣2<x<﹣1时,求反比例函数y=![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com