
ĄŸÌâÄżĄżÎȘÈ«Ăæčáłč”ł”ÄœÌÓę·œŐ룏ŒáłÖĄ°œĄż””ÚÒ»”ÄœÌÓęÀíÄŽÙœűѧÉúœĄż”łÉł€ŁŹÌážßÌćÖÊœĄż”ËźÆœŁŹłÉ¶ŒÊĐ”śŐûÌćÓęÖĐżŒÊ”Ê©·œ°žŁș·ÖÖ”ÔöŒÓÖÁ60ŁŹÄĐ1000ŁšĆź80ĂŚŁ©±ŰżŒŁŹŚăÇòĄąÀșÇòĄąĆĆÇòĄ°ÈęŃĄÒ»Ą±ĄĄŽÓ2019ÄêÇĐÂÈëѧ”ÄÆßÄꌶÆđżȘʌʔʩŁŹÄł1ѧÎȘÁËœâÆßÄêŒ¶Ń§Éú¶ÔÈęŽóÇòÀàÔ˶Ż”ÄÏČ°źÇéżöŁŹŽÓÆßÄêŒ¶Ń§ÉúÖĐËæ»úłéÈĄČż·ÖѧÉúœűĐĐ”śČéÎÊŸíŁŹÍščę·ÖÎöŐûÀí»æÖÆÁËÈçÏÂÁœ·ùÍłŒÆÍŒĄŁÇëžùŸĘÁœ·ùÍłŒÆÍŒÖĐ”ÄĐĆÏą»ŰŽđÏÂÁĐÎÊÌâ:

Łš1Ł©ÇóČÎÓ딜Čé”ÄѧÉúÖĐŁŹÏČ°źĆĆÇòÔ˶Ż”ÄѧÉúÈËÊ꣏ȹČčÈ«ÌőĐÎÍŒ
Łš2Ł©ÈôžĂÖĐѧÆßÄꌶčČÓĐ400ĂûѧÉúŁŹÇëÄăčÀŒÆžĂÖĐѧÆßÄêŒ¶Ń§ÉúÖĐÏČ°źÀșÇòÔ˶Ż”ÄѧÉúÓжàÉÙĂûŁż
Łš3Ł©ÈôŽÓÏČ°źŚăÇòÔ˶Ż”Ä2ĂûÄĐÉúșÍ2ĂûĆźÉúÖĐËæ»úłéÈĄ2ĂûѧÉúŁŹÈ·¶šÎȘžĂĐŁŚăÇòÔ˶ŻÔ±”ÄÖŰ”ăĆàŃű¶ÔÏóŁŹÇëÓĂÁĐ±í·š»ò»ÊśŚŽÍŒ”Ä·œ·šÇółéÈĄ”ÄÁœĂûѧÉúÎȘÒ»ĂûÄĐÉúșÍÒ»ĂûĆźÉú”ÄžĆÂÊ.
ĄŸŽđ°žĄżŁš1Ł©21ŁŹÍŒĐÎŒûœâÎöŁ»Łš2Ł©180Ł»Łš3Ł©![]()
ĄŸœâÎöĄż
Łš1Ł©ÏÈžùŸĘŚăÇòÈËÊęŒ°Æä°Ù·Ö±ÈÇó”ĂŚÜÈËÊ꣏ÔÙÓĂŚÜÈËÊęłËÒÔĆĆÇòÈËÊęŐŒŚÜÈËÊę”Ä°Ù·Ö±ÈżÉ”ĂĆĆÇòÈËÊ꣏ŒŽżÉČčÈ«ÍŒĐÎŁ»
Łš2Ł©žùŸĘŃù±ŸčÀŒÆŚÜÌ棏ÏÈÇółöÏČ°źÀșÇòÔ˶ŻÈËÊę”Ä°Ù·Ö±ÈŁŹÈ»șóÓĂ400łËÒÔÀșÇòÈËÊęŐŒ°Ù·Ö±ÈŁŹŒŽżÉ”Ă”œÏČ°źÀșÇòÔ˶ŻÈËÊꣻ
Łš3Ł©»ÊśŚŽÍŒ”ĂłöËùÓĐ”ÈżÉÄÜ”ÄÇéżöÊ꣏ŐÒłö1ĂûÄĐÉúșÍ1ĂûĆźÉú”ÄÇéżöÊ꣏žùŸĘžĆÂÊč«ÊœŒŽżÉ”ĂłöËùÇóžĆÂÊŁź
œâŁșŁš1Ł©![]() ŁšÈËŁ©ŁŹ
ŁšÈËŁ©ŁŹ
![]() ŁšÈËŁ©.
ŁšÈËŁ©.
ËùÒÔŁŹČÎÓ딜Čé”ÄѧÉúÖĐŁŹÏČ°źĆĆÇòÔ˶Ż”ÄѧÉúÓĐ21ÈË.
ČčÈ«ÌőĐÎÍŒÈçÏÂŁș

Łš2Ł©![]() ŁšÈËŁ©.
ŁšÈËŁ©.
ËùÒÔŁŹžĂÖĐѧÆßÄêŒ¶Ń§ÉúÖĐŁŹÏČ°źÀșÇòÔ˶Ż”ÄѧÉúÓĐ180ÈË.
Łš3Ł©

čČÓĐ12ÖÖ”ÈżÉÄÜÇéżöŁŹŁšÄĐ1ŁŹÄĐ2Ł©ĄąŁšÄĐ1ŁŹĆź1Ł©ĄąŁšÄĐ1ŁŹĆź2Ł©ĄąŁšÄĐ2ŁŹÄĐ1Ł©ĄąŁšÄĐ2ŁŹĆź1Ł©ĄąŁšÄĐ2ŁŹĆź2Ł©ĄąŁšĆź1ŁŹÄĐ1Ł©ĄąŁšĆź1ŁŹÄĐ2Ł©ĄąŁšĆź1ŁŹĆź2Ł©ĄąŁšĆź2ŁŹÄĐ1Ł©ĄąŁšĆź2ŁŹÄĐ2Ł©ĄąŁšĆź2ŁŹĆź1Ł©ŁŹÆäÖĐŁŹ1ĂûÄĐÉúșÍ1ĂûĆźÉúÓĐ8ÖÖ.
ËùÒÔŁŹłé”œ1ĂûÄĐÉúșÍ1ĂûĆźÉú”ÄžĆÂÊ![]() .
.



| Äꌶ | žßÖĐżÎłÌ | Äꌶ | łőÖĐżÎłÌ |
| žßÒ» | žßÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ | łőÒ» | łőÒ»Ăâ·ŃżÎłÌÍÆŒöŁĄ |
| žß¶ț | žß¶țĂâ·ŃżÎłÌÍÆŒöŁĄ | łő¶ț | łő¶țĂâ·ŃżÎłÌÍÆŒöŁĄ |
| žßÈę | žßÈęĂâ·ŃżÎłÌÍÆŒöŁĄ | łőÈę | łőÈęĂâ·ŃżÎłÌÍÆŒöŁĄ |
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘ¶țŽÎșŻÊęyŁœkx2+Łšk+1Ł©x+1ŁškĄÙ0Ł©Łź
Łš1Ł©ÇóÖ€ŁșÎȚÂÛkÈĄÈÎșÎÊ”ÊęʱŁŹžĂșŻÊęÍŒÏóÓëxÖáŚÜÓĐœ»”㣻
Łš2Ł©ÈçčûžĂșŻÊę”ÄÍŒÏóÓëxÖ᜻”ă”ÄșáŚű±êŸùÎȘŐûÊ꣏ÇÒkÎȘŐûÊ꣏ÇókÖ”Łź
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚÆœĂæÖ±œÇŚű±êÏ”ÖĐŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ
ŁŹ![]() ŁŹ”ă
ŁŹ”ă![]() ”ÄŚű±êÎȘ
”ÄŚű±êÎȘ![]() .ĆŚÎïÏß
.ĆŚÎïÏß![]() Ÿčę
Ÿčę![]() Ąą
Ąą![]() Áœ”ă.
Áœ”ă.
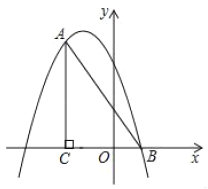
Łš1Ł©ÇóĆŚÎïÏߔĜâÎöÊœŁ»
Łš2Ł©”ă![]() ÊÇÖ±Ïß
ÊÇÖ±Ïß![]() ÉÏ·œĆŚÎïÏßÉÏ”ÄÒ»”㣏čę”ă
ÉÏ·œĆŚÎïÏßÉÏ”ÄÒ»”㣏čę”ă![]() Śś
Śś![]() ŽčÖ±
ŽčÖ±![]() ÖáÓÚ”ă
ÖáÓÚ”ă![]() ŁŹœ»Ï߶Î
ŁŹœ»Ï߶Î![]() ÓÚ”ă
ÓÚ”ă![]() ŁŹÊč
ŁŹÊč![]() ŚîŽó.
ŚîŽó.
ąÙÇó”ă![]() ”ÄŚű±êșÍ
”ÄŚű±êșÍ![]() ”ÄŚîŽóÖ”.
”ÄŚîŽóÖ”.
ąÚÔÚÖ±Ïß![]() ÉÏÊÇ·ńŽæÔÚ”ă
ÉÏÊÇ·ńŽæÔÚ”ă![]() ŁŹÊč”ă
ŁŹÊč”ă![]() ÔÚÒÔ
ÔÚÒÔ![]() ÎȘÖ±Ÿ¶”ÄÔČÉÏŁ»ÈôŽæÔÚŁŹÇółö”ă
ÎȘÖ±Ÿ¶”ÄÔČÉÏŁ»ÈôŽæÔÚŁŹÇółö”ă![]() ”ÄŚű±êŁŹÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉ.
”ÄŚű±êŁŹÈôČ»ŽæÔÚŁŹÇë˔ÜÀíÓÉ.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÒŃÖȘABÊÇ°ëÔČO”ÄÖ±Ÿ¶ŁŹMŁŹNÊÇ°ëÔČÉÏČ»ÓëAŁŹBÖŰșÏ”ÄÁœ”㣏ÇÒ”ăNÔÚ![]() ÉÏ.
ÉÏ.
Łš1Ł©ÈçÍŒ1ŁŹMAŁœ6ŁŹMBŁœ8ŁŹĄÏNOBŁœ60ĄăŁŹÇóNB”Äł€Ł»

Łš2Ł©ÈçÍŒ2ŁŹčę”ăMŚśMCĄÍABÓÚ”ăCŁŹPÊÇMN”ÄÖД㣏ÁŹœÓMBŁŹNAŁŹPCŁŹÊÔÌœŸżĄÏMCPŁŹĄÏNABŁŹĄÏMBAÖźŒä”ÄÊęÁżčŰÏ”ŁŹČąÖ€Ăś.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
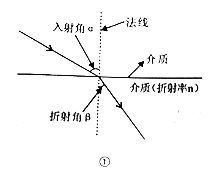
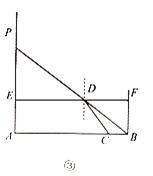
ĄŸÌâÄżĄżčâÏߎӿŐÆűÉäÈëËźÖл᷹ÉúŐÛÉäÏÖÏóŁŹ·ąÉúŐÛÉäʱŁŹÂúŚă”ÄŐÛÉ䶚ÂÉÈçÍŒąÙËùÊŸŁșŐÛÉäÂÊ![]() Łš
Łš![]() Žú±íÈëÉäœÇŁŹ
Žú±íÈëÉäœÇŁŹ![]() Žú±íŐÛÉäœÇŁ©.ĐĄĂśÎȘÁËčÛČìčâÏß”ÄŐÛÉäÏÖÏóŁŹÉèŒÆÁËÍŒąÚËùÊŸ”ÄÊ”Ń飻͚čęÏžčÜżÉÒÔżŽŒûËź”Ś”ÄÎïżéŁŹ”«ŽÓÏžčÜŽ©čę”ÄÖ±ÌúËżŁŹÈŽĆöČ»ÉÏÎïżéŁŹÍŒąÛÊÇÊ”Ńé”ÄÊŸÒâÍŒŁŹ”ăA,C,BÔÚÍŹÒ»Ö±ÏßÉÏŁŹČâ”Ă
Žú±íŐÛÉäœÇŁ©.ĐĄĂśÎȘÁËčÛČìčâÏß”ÄŐÛÉäÏÖÏóŁŹÉèŒÆÁËÍŒąÚËùÊŸ”ÄÊ”Ń飻͚čęÏžčÜżÉÒÔżŽŒûËź”Ś”ÄÎïżéŁŹ”«ŽÓÏžčÜŽ©čę”ÄÖ±ÌúËżŁŹÈŽĆöČ»ÉÏÎïżéŁŹÍŒąÛÊÇÊ”Ńé”ÄÊŸÒâÍŒŁŹ”ăA,C,BÔÚÍŹÒ»Ö±ÏßÉÏŁŹČâ”Ă![]() ŁŹÔòčâÏߎӿŐÉäÈëËźÖĐ”ÄŐÛÉäÂÊn”ÈÓÚ________.
ŁŹÔòčâÏߎӿŐÉäÈëËźÖĐ”ÄŐÛÉäÂÊn”ÈÓÚ________.

Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒŁŹÔÚŐę·œĐÎÍűžńÖĐŁŹĄśABC”ÄÈęžö¶„”ă¶ŒÔÚžń”ăÉÏŁŹ”ăAĄąBĄąC”ÄŚű±ê·Ö±đÎȘŁšŁ2ŁŹ4Ł©ĄąŁšŁ2ŁŹ0Ł©ĄąŁšŁ4ŁŹ1Ł©ŁŹœáșÏËùžű”ÄÆœĂæÖ±œÇŚű±êÏ”œâŽđÏÂÁĐÎÊÌâŁș
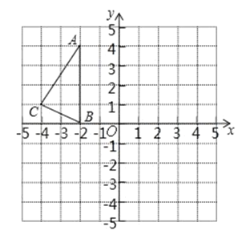
Łš1Ł©œ«ĄśABCÈÆO”ăÄæʱŐëĐęŚȘ90ĄăŁŹ”Ă”œĄśA1B1C1Ł»
Łš2Ł©ÒÔ”ăPŁšŁ1ŁŹ1Ł©ÎȘλËÆÖĐĐÄŁŹÔÚĄśABC”ÄÒìČàŚśÎ»ËƱ任ŁŹÇÒÊ襜ABC”ÄĂæ»ęÀ©ŽóÎȘÔÀŽ”Ä4±¶ŁŹ”Ă”œĄśA2B2C2ŁŹČąĐŽłö”ăA2”ÄŚű±ê.
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżŁš3·ÖŁ©ÈçÍŒŁŹŐę·œĐÎABCD”ı߳€ÎȘ3cmŁŹ¶Ż”ăPŽÓB”ăłö·ąÒÔ3cm/s”ÄËÙ¶ÈŃیƱßBC©CD©DAÔ˶ŻŁŹ”œŽïA”ăÍŁÖčÔ˶ŻŁ»ÁíÒ»¶Ż”ăQÍŹÊ±ŽÓB”ăłö·ąŁŹÒÔ1cm/s”ÄËÙ¶ÈŃیƱßBAÏòA”ăÔ˶ŻŁŹ”œŽïA”ăÍŁÖčÔ˶ŻŁźÉèP”ăÔ˶ŻÊ±ŒäÎȘxŁšsŁ©ŁŹĄśBPQ”ÄĂæ»ęÎȘyŁšcm2Ł©ŁŹÔòyčŰÓÚx”ÄșŻÊęÍŒÏóÊÇŁš Ł©
AŁź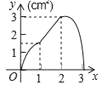 BŁź
BŁź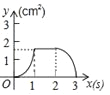 CŁź
CŁź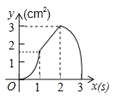 DŁź
DŁź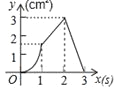
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
ĄŸÌâÄżĄżÈçÍŒËùÊŸŁŹÍőžŐ͏ѧËùÔÚ”ÄŃ§Ï°ĐĄŚéÓûČâÁżĐŁÔ°ÀïÒ»żĂŽóÊś”Äžß¶ÈŁŹËûĂÇŃĄÍőžŐŚśÎȘčÛČâŐߣŹČąÔÚÍőžŐÓëŽóÊśÖźŒä”Ä”ŰĂæÉÏÖ±ÁąÒ»žùžßÎȘ2m”ıêžËCDŁŹÈ»șóŁŹÍőžŐżȘÊŒ”śŐûŚÔŒș”ÄλÖĂŁŹ”±ËûżŽ”œ±êžË”Ķ„¶ËCÓëÊś”Ķ„¶ËEÖŰșÏʱŁŹŸÍÔÚžĂλÖĂÍŁÖčČ»¶ŻŁŹŐâʱÆäËû͏ѧ͚čęČâÁżŁŹ·ąÏÖÍőžŐ”ÄœĆÀë±êžË”ŚČż”ÄŸàÀëÎȘ1mŁŹÀëŽóÊś”ŚČż”ÄŸàÀëÎȘ9mŁŹÍőžŐ”ÄŃÛÀë”ŰĂæ”Ğ߶ÈABÎȘ1.5mŁŹÄÇĂŽŽóÊśEF”ÄžßÎȘ¶àÉÙŁż
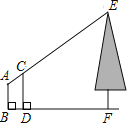
Č鿎Žđ°žșÍœâÎö>>
żÆÄżŁșłőÖĐÊęѧ ÀŽÔŽŁș ÌâĐÍŁș
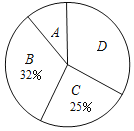
ĄŸÌâÄżĄżÔÚĄ°ÊéÏăĐŁÔ°Ą±»î¶ŻÖĐŁŹÄłĐŁÎȘÁËœâѧÉúŒÒÍ„ČŰÊéÇéżöŁŹËæ»úłéÈĄ±ŸĐŁČż·ÖѧÉúœűĐĐ”śČ飏ȹ»æÖÆłÉČż·ÖÍłŒÆÍŒ±íÈçÏÂŁș
Àà±đ | ŒÒÍ„ČŰÊém±Ÿ | ѧÉúÈËÊę |
A | 0ĄÜmĄÜ25 | 20 |
B | 26ĄÜmĄÜ50 | a |
C | 51ĄÜmĄÜ75 | 50 |
D | mĄĘ76 | 66 |
žùŸĘÒÔÉÏĐĆÏąŁŹœâŽđÏÂÁĐÎÊÌâŁș
Łš1Ł©žĂ”śČé”ÄŃù±ŸÈĘÁżÎȘĄĄ ĄĄŁŹaŁœĄĄ ĄĄŁ»
Łš2Ł©Ëæ»úłéÈĄÒ»Î»Ń§ÉúœűĐĐ”śČ飏žŐșĂłé”œAÀàѧÉú”ÄžĆÂÊÊÇĄĄ ĄĄŁ»
Łš3Ł©ÈôžĂĐŁÓĐ2000ĂûѧÉúŁŹÇëčÀŒÆÈ«ĐŁŃ§ÉúÖĐŒÒÍ„ČŰÊéČ»ÉÙÓÚ76±Ÿ”ÄÈËÊ꣟
Č鿎Žđ°žșÍœâÎö>>
°Ù¶ÈÖÂĐĆ - Á·Ï°ČáÁбí - ÊÔÌâÁбí
șț±±ÊĄ»„ÁȘÍű΄·šșÍČ»ÁŒĐĆÏąŸÙ±šÆœÌš | ÍűÉÏÓĐșŠĐĆÏąŸÙ±šŚšÇű | ”çĐĆŐ©ÆŸÙ±šŚšÇű | ÉæÀúÊ·ĐéÎȚÖśÒćÓĐșŠĐĆÏąŸÙ±šŚšÇű | ÉæÆóÇÖÈšŸÙ±šŚšÇű
΄·šșÍČ»ÁŒĐĆÏąŸÙ±š”ç»°Łș027-86699610 ŸÙ±šÓÊÏäŁș58377363@163.com