
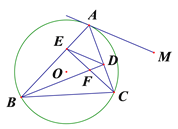
【题目】如图,△ABC是⊙O的内接三角形,CE⊥AB于点E,BD⊥AC于点D,BD、CE相交于点F,连结ED.
(1)若∠ABC=45°,证明AE=EF;
(2)求证:△AED∽△ACB;
(3)过点A的直线AM∥ED, AM是⊙O的切线吗?说明理由.
【答案】(1)证明见解析;(2)证明见解析;(3)是,证明见解析.
【解析】试题分析:(1)由ASA证明△BEF≌△CEA即可;
(2)先证明△AEC∽△ADB,得到AE:AD=AC:AB,再证明△AED∽△ACB即可;
(3)连接AO并延长交⊙O于N,连接NC.由△AED∽△ACB,得到∠ADE=∠ABC,由同弧所对的圆周角相等,得到∠ABC=∠N,等量代换得到∠ADE=∠N.由平行线的性质得到∠MAC=∠ADE,从而∠MAC=∠N.由AN为直径,得到∠CAN+∠N=90°,进而∠CAN+∠MAC=90°,即可得到结论.
试题解析:解:(1)∵∠ABC=45°,CE⊥AB,即∠BEC=90°,∴∠ECB=45°=∠EBC,∴EB=EC.
∵CE⊥AB,BD⊥AC,∴∠BEC=∠BDC=90°,∴∠EBF+∠EFB=90°,∠DFC+∠DCF=90°.
∵∠EFB=∠DFC,∴∠EBF=∠DCF.
在△BEF和△CEA中,∵∠FBE=∠ACE,BE=CE,∠BEF=∠CEA=90°,∴△BEF≌△CEA,∴AE=EF.
(2)∵∠EBF=∠DCF,∠A=∠A,∴△AEC∽△ADB,∴AE:AD=AC:AB.∵∠A=∠A,∴△AED∽△ACB;
(3)AM是⊙O的切线.理由如下:
连接AO并延长交⊙O于N,连接NC.∵△AED∽△ACB,∴∠ADE=∠ABC.∵∠ABC=∠N,∴∠ADE=∠N.∵AM∥ED,∴∠MAC=∠ADE,∴∠MAC=∠N.∵AN为直径,∴∠NCA=90°,∴∠CAN+∠N=90°,∴∠CAN+∠MAC=90°,∴∠MAO=90°,∴AM是⊙O的切线.



科目:初中数学 来源: 题型:
【题目】已知a是最大的负整数,b、c满足![]() ,且a,b,c分别是点A,B,C在数轴上对应的数.
,且a,b,c分别是点A,B,C在数轴上对应的数.
(1)求a,b,c的值,并在数轴上标出点A,B,C;
![]()
(2)若动点P从C出发沿数轴正方向运动,点P的速度是每秒2个单位长度,运动几秒后,点P到达B点?
(3)在数轴上找一点M,使点M到A,B,C三点的距离之和等于13,请直接写出所有点M对应的数.(不必说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在一次数学活动课上,张明用17个边长为1的小正方形搭成了一个几何体,然后他请王亮用其他同样的小正方体在旁边再搭一个几何体,使王亮所搭几何体恰好可以和张明所搭几何体拼成一个无缝隙的大长方体(不改变张明所搭几何体的形状),那么王亮至少还需要 个小立方体,王亮所搭几何体的表面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把边长为1的10个相同正方体摆成如图的形式.
(1)画出该几何体的主视图、左视图、俯视图;
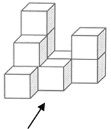
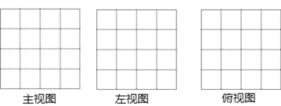
(2)试求出其表面积(包括向下的面);
(3)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的左视图和俯视图不变,那么最多可以再添加 个小正方体.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上有A,B两点,分别对应的数为a,b。| a |=3,| b |=9,
![]()
(1)求a与b的值。
(2)求出线段AB的长度。
(3)若数轴上有一点C,且C到B的距离是C到A距离的3倍,直接写出点C所表示的数。
(4)点P从点A出发,先向左移动1个单位长度,再向右移动2个单位长度,再向左移动3个单位长度,再向右移动4个单位长度········,求出1889次移动后的点P所表示的数
查看答案和解析>>
科目:初中数学 来源: 题型:
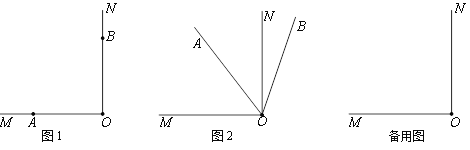
【题目】如图1,∠MON=90°,点A,B分别在射线OM、ON上.将射线OA绕点O沿顺时针方向以每秒9°的速度旋转,同时射线OB绕点O沿顺时针方向以每秒3°的速度旋转(如图2).设旋转时间为t(0≤t≤40,单位秒).
(1)当t=8时,∠AOB= °;
(2)在旋转过程中,当∠AOB=36°时,求t的值.
(3)在旋转过程中,当ON、OA、OB三条射线中的一条恰好平分另外两条射线组成的角(指大于0°而不超过180°的角)时,请求出t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某影院共有15排座位,第一排有12个座位数,从第2排开始,每一排都比前一排增加2个座位.
(1)请你在下表的空格里填写一个适当的式子.
第1排的座位数 | 第2排的座位数 | 第3排的座位数 | … | 第 |
12 | 14 | 16 | … |
(2)影院最后两排共有多少个座位?
查看答案和解析>>
科目:初中数学 来源: 题型:
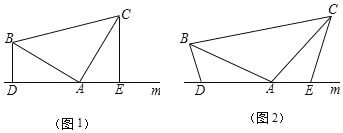
【题目】(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,证明:△ABD≌△ACE,DE=BD+CE;
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D, A, E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=a,其中a为任意锐角或钝角,请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育委员统计了全班同学60秒跳绳的次数,列出了频数分布表和频数分布直方图,如图:
次数 | 频数 |
| 2 |
| |
| 18 |
| 13 |
| 8 |
| |
| 1 |
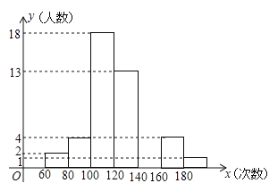
(1)补全频数分布表和频数分布直方图.
(2)上表中组距是__________次,组数是___________组.
(3)跳组次数在![]() 范围的学生有__________人,全班共有___________人.
范围的学生有__________人,全班共有___________人.
(4)若规定跳维次数不低于140次为优秀,求全班同学跳绳的优秀率是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com