练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    6．如图，已知矩形ABCD中，R、P分别是DC、BC上的点，E、F分别是AP、RP的中点，当点P在BC上从B向C移动而R不动时，那么下列结论成立的是（　　）
    A．线段EF的长不能确定B．线段EF的长逐渐增大
    C．线段EF的长逐渐减小D．线段EF的长不改变

    分析 因为R不动，所以AR不变．根据中位线定理，EF不变．

    解答 解：连接AR，
    ∵E、F分别是AP、RP的中点，
    ∴EF为△APR的中位线，
    ∴EF=$\frac{1}{2}$AR，
    ∵AR的长为定值．
    ∴线段EF的长不改变，
    故选D．

    点评 本题考查了三角形的中位线定理，只要三角形的边AR不变，则对应的中位线的长度就不变．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

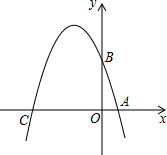    1．已知如图，在平面直角坐标系xOy中，点A、B、C分别为坐标轴上的三个点，且OA=1，OB=3，OC=4，
    （1）求经过A、B、C三点的抛物线的解析式；
    （2）在平面直角坐标系xOy中是否存在一点P，使得以点A、B、C、P为顶点的四边形为菱形？若存在，请求出点P的坐标；若不存在，请说明理由；
    （3）若点M为该抛物线上一动点，在（2）的条件下，请求出当|PM-AM|的最大值时点M的坐标，并直接写出|PM-AM|的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    17．如图，某厂房屋顶钢架外框是等腰三角形，其中AB=AC，D，E，F分别是BC，AB，AC的中点．已知AB=8m，求DE+DF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

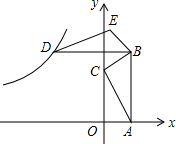    14．如图，在平面直角坐标系上，△ABC的顶点A和C分别在x轴、y轴的正半轴上，且AB∥y轴，点B（1，3），将△ABC以点B为旋转中心顺时针方向旋转90°得到△DBE，恰好有一反比例函数y=$\frac{k}{x}$图象恰好过点D，则k的值为（　　）
    A．6B．-6C．9D．-9

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    1．下列说法正确的是（　　）
    A．为了解某中学800名学生的视力情况，从中随机抽取了50名学生进行调查，在此调查中，样本容量为50名学生的视力
    B．若一个游戏的中奖率是1%，则做100次这样的游戏一定会中奖
    C．了解无锡市每天的流动人口数，采用抽查方式
    D．“掷一枚硬币，正面朝上”是必然事件

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

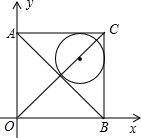    11．如图，在平面直角坐标系中有一正方形AOBC，反比例函数y=$\frac{k}{x}$经过正方形AOBC对角线的交点，半径为4-2$\sqrt{2}$的圆内切于△ABC，则k的值为（　　）
    A．$\sqrt{2}$B．2C．4D．2$\sqrt{2}$

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．某网店尝试用单价随天数而变化的销售模式销售一种商品，利用30天的时间销售一种成本为10元/件的商品售后，经过统计得到此商品单价在第x天（x为正整数）销售的相关信息，如表所示：
    销售量n（件）n=50-x
    销售单价m（元/件）当1≤x≤20时，m=20+$\frac{1}{2}$x
    当21≤x≤30时，m=10+$\frac{420}{x}$
    （1）请计算第几天该商品单价为25元/件？
    （2）求网店销售该商品30天里所获利润y（元）关于x（天）的函数关系式；
    （3）这30天中第几天获得的利润最大？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．下列说法正确的是（　　）
    A．掷一枚均匀的骰子，骰子停止转动后，6点朝上是必然事件
    B．“直角三角形三条边中垂线的交点是斜边的中点”这是必然事件
    C．“明天降雨的概率为$\frac{1}{2}$”表示明天有半天都在降雨
    D．了解一批电视机的使用寿命，适合用普查的方法

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    16．某电视台为了解本地区电视节目的收视率情况，对部分观众开展了“你最喜爱的电视节目”的问卷调查（每人只填写一项），根据收集的数据绘制了下面两副不完整的统计图，根据要求回答下列问题：
    （1）本次问卷调查共调查了多少名观众？请补全条形统计图并在图中标明相应数据；
    （2）请分别求出图2中收看“综艺节目”的人数占调查中人数的百分比，“科普节目”在扇形图中所对应的圆心角的度数；
    （3）现有喜欢“新闻节目”（记为A），“体育节目”（记为B），“综艺节目”（记为C），“科普节目”（记为D）的观众各一名，电视台要从四人中随机抽取两人参加联谊活动，请用“列表法”或“画树形图”的方法求出恰好抽到喜欢“新闻节目”和“体育节目”的两位观众的概率．

    查看答案和解析>>

    同步练习册答案