
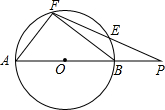
 如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.
如图,点P在⊙O的直径AB的延长线上,PEF是⊙O的割线,且AF=FE,$\frac{PB}{PE}=\frac{5}{6}$,△ABF的面积为96.分析 (1)连接AE,作FH⊥AE于H,如图1,利用圆周角定理得∠EFB=∠EAP,则可证明△PFB∽△PAE,利用相似比得$\frac{PB}{PE}$=$\frac{FB}{AE}$=$\frac{5}{6}$,设FB=5a,则AE=6a,再利用等腰三角形的性质得AH=HE=$\frac{1}{2}$AE=3a,∠FAE=∠FEA,接着证明Rt△AFH∽Rt△BAF得到$\frac{FH}{AF}$=$\frac{AH}{BF}$=$\frac{3a}{5a}$=$\frac{3}{5}$,设FH=3t,AF=5t,根据勾股定理得(3a)2+(3t)2=(5t)2,解得t=$\frac{3}{4}$a,所以AF=5t=$\frac{15}{4}$a,然后根据三角形面积公式可计算出a=$\frac{16}{5}$,所以AF=$\frac{15}{4}$a=12,BF=5a=16,原式利用勾股定理可计算出AB=20;
(2)作FC⊥AB于C,如图2,利用面积法计算出FC=$\frac{48}{5}$,再根据切割线定理得PE•PF=PB•PA,所以$\frac{PB}{PE}$=$\frac{PF}{PA}$=$\frac{PE+12}{PB+20}$=$\frac{5}{6}$,则利用比例的性质可求出PE=$\frac{168}{11}$,所以PF=EF+PE=$\frac{300}{11}$,然后在Rt△PFC中利用正弦的定义求解.
解答 解:(1)连接AE,作FH⊥AE于H,如图1,
∵∠EFB=∠EAP,
∵∠P=∠P,
∴△PFB∽△PAE,
∴$\frac{PB}{PE}$=$\frac{FB}{AE}$=$\frac{5}{6}$,
设FB=5a,则AE=6a,
∵AF=EF,FH⊥AE,
∴AH=HE=$\frac{1}{2}$AE=3a,∠FAE=∠FEA,
∵∠ABF=∠FEA,
∴∠FAE=∠FBA,
∵AB为直径,
∴∠AFB=90°,
∴Rt△AFH∽Rt△BAF,
∴$\frac{FH}{AF}$=$\frac{AH}{BF}$=$\frac{3a}{5a}$=$\frac{3}{5}$,
设FH=3t,AF=5t,
在Rt△AHF中,(3a)2+(3t)2=(5t)2,解得t=$\frac{3}{4}$a,
∴AF=5t=$\frac{15}{4}$a,
∵△ABF的面积为96,
∴$\frac{1}{2}$•$\frac{15}{4}$a•5a=96,解得a=$\frac{16}{5}$,
∴AF=$\frac{15}{4}$a=12,BF=5a=16,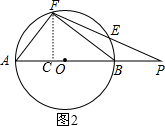
在Rt△ABF中,AB=$\sqrt{1{2}^{2}+1{6}^{2}}$=20;
(2)作FC⊥AB于C,如图2,
∵$\frac{1}{2}$FC•AB=$\frac{1}{2}$AF•BF,
∴FC=$\frac{12×16}{20}$=$\frac{48}{5}$,
∵PE•PF=PB•PA,
∴$\frac{PB}{PE}$=$\frac{PF}{PA}$=$\frac{PE+12}{PB+20}$=$\frac{5}{6}$,
∴PE=$\frac{168}{11}$,
∴PF=EF+PE=12+$\frac{168}{11}$=$\frac{300}{11}$,
在Rt△PFC中,sin∠P=$\frac{FC}{PF}$=$\frac{\frac{48}{5}}{\frac{300}{11}}$=$\frac{44}{125}$.
点评 本题考查了圆的综合题:熟练掌握圆周角定理和切割线定理;会运用相似三角形的性质计算线段的长和求线段之间的关系;会利用勾股定理和三角形面积公式计算.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )
如图,已知AD为△ABC的高线,AD=BC,以AB为底边作等腰Rt△ABE,连接ED,EC,延长CE交AD于F点,下列结论:①△ADE≌△BCE;②CE⊥DE;③BD=AF;④S△BDE=S△ACE,其中正确的有( )| A. | ①③ | B. | ①②④ | C. | ①②③④ | D. | ①③④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com