
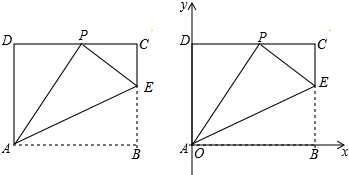
分析 (1)根据矩形的性质得到AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°,根据折叠的性质和相似三角形的判定定理证明结论;
(2)根据相似三角形的面积比等于相似比的平方得到$\frac{EC}{PD}$=$\frac{EP}{PA}$=$\frac{CP}{DA}$=$\frac{1}{2}$,设EP=x,根据勾股定理列出方程,解方程得到答案;
(3)根据题意和分情况讨论思想画出图形,根据平行四边形的判定定理求出点M的坐标.
解答 解:(1)∵四边形ABCD是矩形,
∴AD=BC,DC=AB,∠DAB=∠B=∠C=∠D=90°,
由折叠的性质可知,AP=AB,PE=BE,∠PAE=∠BAE,∠APE=∠B,
∴∠APE=90°,
∴∠APD=∠PEC,
∴△ECP∽△PDA;
(2)△ECP与△PDA的面积比为1:4,
∴$\frac{EC}{PD}$=$\frac{EP}{PA}$=$\frac{CP}{DA}$=$\frac{1}{2}$,
∴PD=2EC,PA=2EP,DA=2CP,
∵AD=8,
∴CP=4,
设EP=x,则EB=x,CE=8-x,
由勾股定理得,x2=(8-x)2+42,
解得,x=5,
∴AB=AP=2EP=10,
∴边AB的长为10;
(3)如图,以OB、BE为邻边时,AM′=BE=5,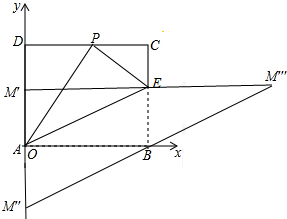
∴M′的坐标为(0,5),
以BE为边、AB为对角线时,
AM′′=BE=5,
∴M′′的坐标为(0,-5),
以AB为边、BE为对角线时,
M′M′′′=2AB=20,
∴M′′′的坐标(20,5).
点评 本题考查的是矩形的性质、相似三角形的性质和折叠的性质,掌握相似三角形的面积比等于相似比的平方、翻折变换的性质是对应角相等、对应边相等是解题的关键,注意数形结合思想的正确运用.


 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
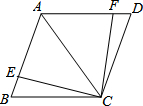 (1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.
(1)如图,AC是菱形ABCD的对角线,点E、F分别在边AB、AD上,且AE=AF.求证:△ACE≌△ACF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
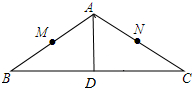 如图,△ABC中,AB=AC=6cm,∠BAC=120°,M、N分趴是AB,AC的中点,AD⊥BC,垂足为D,以D为圆心,3cm为半径画圆,判断A,B,C,M,N各点和⊙D的位置关系.
如图,△ABC中,AB=AC=6cm,∠BAC=120°,M、N分趴是AB,AC的中点,AD⊥BC,垂足为D,以D为圆心,3cm为半径画圆,判断A,B,C,M,N各点和⊙D的位置关系.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
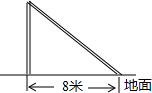 如图,台风过后,一颗白杨树在高地某处断裂,白杨树的顶部落在离白杨树根部8米处,已知白杨树高16米,你能求出白杨树在离根部多少米的位置断裂吗?
如图,台风过后,一颗白杨树在高地某处断裂,白杨树的顶部落在离白杨树根部8米处,已知白杨树高16米,你能求出白杨树在离根部多少米的位置断裂吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com