
【题目】如图,正方形ABCD的面积为16cm2,△AEF为等腰直角三角形,∠E=90°,AE和BC交于点G,AF和CD交于点H,则△CGH的周长( )

A. 4cmB. 6cmC. 8cmD. 10cm
【答案】C
【解析】
延长CB至M,使BM=DH,连接AM;易证△ABM≌△ADH与△AMG≌△AHG,得到△CGH的周长=GH+CG+CH=GM+CG+CH=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=8.
延长CB至M,使BM=DH,连接AM;如图所示:
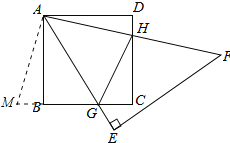
∵四边形ABCD是正方形,正方形ABCD的面积为16cm2,
∴AB=BC=CD=4cm,∠BAD=∠ABC=∠D=90°,
∴∠ABM=90°,
在△ABM和△ADH中,AB=AD,∠ABM=∠D=90°,BM=DH,
∴△ABM≌△ADH(SAS),
∴AM=AH,∠BAM=∠DAH,
∵△AEF是等腰直角三角形,
∴∠HAG=45°,
∴∠BAG+∠DAH=45°,
∴∠MAG=45°,
在△AMG和△AHG中,AM=AH,∠MAG=∠HAG,AG=AG
∴△AMG≌△AHG(SAS),
∴GM=GH,
∴△CGH的周长=GH+CG+CH=GM+CG+CH
=BM+BG+CG+CH=DH+BG+CG+CH=BC+CD=8.
故选:C.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:
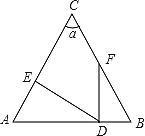
【题目】如图∠A=∠B,∠C=![]() ,DE⊥AC于点E,FD⊥AB于点D.
,DE⊥AC于点E,FD⊥AB于点D.
(1)若∠EDA=25°,则∠EDF=________°;
(2)若∠A=65°,则∠EDF=_______°;
(3)若![]() =50°,则∠EDF=_______°;
=50°,则∠EDF=_______°;
(4)若∠EDF=65°,则![]() _______°;
_______°;
(5)∠EDF与![]() 的关系为_______.
的关系为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x,y的方程组
(1)若a=2,请直接写出此时方程组的解;
(2)若方程组的解满足x+y=6,求a的值;
(3)若方程组的解x,y的值都为非负数,求2x-y的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四幅图象分别表示变量之间的关系,请按图象的顺序,将下面的四种情境与之对应排序.正确的顺序是( )

①篮球运动员投篮时,投出去的篮球的高度与时间的关系;
②去超市购买同一单价的水果,所付费用与水果数量的关系;
③李老师使用的是一种含月租的手机计费方式,则他每月所付话费与通话时间的关系;
④周末,小明从家到图书馆,看了一段时间书后,按原速度原路返回,小明离家的距离与时间的关系
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O是△ABC的外接圆,∠ABC=45°,AD是⊙O的切线交BC的延长线于D,AB交OC于E.

(1)求证:AD∥OC;
(2)若AE=2![]() ,CE=2.求⊙O的半径和线段BE的长.
,CE=2.求⊙O的半径和线段BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
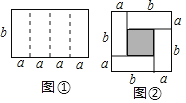
【题目】如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②)
自主探索:
(1)仔细观察图形,完成下列问题
①图②中的阴影部分的面积为_____;
②观察图②,请你写出(a+b)2、(a-b)2、ab之间的等量关系是_____;
知识运用:
(2)若x-y=5,xy=![]() ,根据(1)中的结论,求(x+y)2的值;
,根据(1)中的结论,求(x+y)2的值;
知识延伸
(3)根据你探索发现的结论,完成下列问题:
设A=![]() ,B=x+2y-3
,B=x+2y-3
计算(A-B)2-(A+B)2的结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
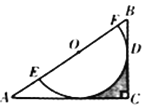
【题目】如图,在Rt△ABC中,∠C=90°,O为AB边上一点,⊙O交AB于点E,F两点,BC切⊙O于点D,且CD=![]() EF=1,
EF=1,
(1)求证:AC与⊙O相切;
(2)求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
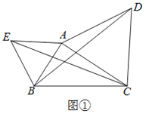
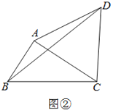
【题目】△ABC中,BC=8,以AC为边向外作等边△ACD.
(1)如图①,△ABE是等边三角形,若AC=6,∠ACB=30°,求CE的长;
(2)如图②,若∠ABC=60°,AB=4,求BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com