
【题目】某校学生准备购买标价为50元的《现代汉语词典》,现有甲、乙两书店出售此书,甲店按如下方法促销:若只购1本,则按原价销售;若一次性购买多于1本,但不多于30本时,每多购一本,售价在标价的基础上优惠2%(例如买2本,每本售价优惠2%;买三本,每本售价优惠4%,以此类推);若多于30本,每本售价20元.乙书店一律按标价的6折销售.
(1)分别写出在两书店购买此书总价y甲、y乙与购书本数x之间的函数关系式;
(2)若这些学生一次性购买多于30本时,那么去哪家书店购买更划算,为什么?若要一次性购买不多于30本时,先写出y(y=y甲﹣y乙)与购买本数x之间的函数式,画出其图象,再利用函数图象分析去哪家书店购买更划算.
【答案】(1)y甲=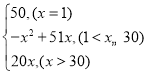 ,y乙=30x;(2)大于30本时到甲书店购买更合算;y=
,y乙=30x;(2)大于30本时到甲书店购买更合算;y=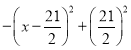 ,若购书少于21本,则到乙书店购买更合算;若购书21本,到甲,乙购书的费用一样;若购书超过21本但不多于30本,则到甲书店购书更合算.图象见解析.
,若购书少于21本,则到乙书店购买更合算;若购书21本,到甲,乙购书的费用一样;若购书超过21本但不多于30本,则到甲书店购书更合算.图象见解析.
【解析】
(1)分别根据两个书店购书的优惠方案得出y与x的函数关系式即可;
(2)首先得出y与x的函数关系式,进而画出图象,利用图象分析得出答案.
解:(1)设购买x本,当x=1时,y甲=50;当![]() 时,
时,![]() ;当x>30时,y甲=20x.
;当x>30时,y甲=20x.
故在甲书店购书的总费用为:
y甲=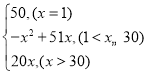 ,
,
在乙书店购书的总费用为:y乙=50×0.6x=30x;
(2)当x>30时,显然y甲<y乙,即到甲书店购买更合算,
当1<x≤30时,y=y甲﹣y乙=﹣x2+51x﹣30x=﹣x2+21x=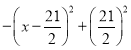 ,
,
当﹣x2+21x=0时,解得:x1=0,x2=21,故函数图象如下:
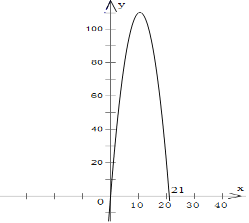
由图象可得出:当1<x<21时,y>0,
当x=21时,y=0,
当30>x>21时,y<0,
综上所述,若购书少于21本,则到乙书店购买更合算;若购书21本,到甲,乙购书的费用一样;若购书超过21但不多于30本,则到甲书店购书更合算.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点都在方格线的交点(格点)上.
(1)将△ABC绕C点按逆时针方向旋转90°得到△A′B′C′,请在图中画出△A′B′C′.
(2)将△ABC向上平移1个单位,再向右平移5个单位得到△A″B″C″,请在图中画出△A″B″C″.
(3)若将△ABC绕原点O旋转180°,A的对应点A1的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
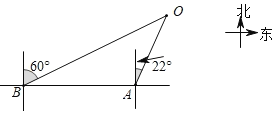
【题目】2019年4月23日是中国人民解放军海军成立70周年纪念日,届时将在青岛举行盛大的多国海军庆祝活动.为此我国海军进行了多次军事演习.如图,在某次军事演习时,舰艇A发现在他北偏东22°方向上有不明敌舰在指挥中心O附近徘徊,快速报告给指挥中心,此时在舰艇A正西方向50海里处的舰艇B接到返回指挥中心的行动指令,舰艇B迅速赶往在他北偏东60°方向的指挥中心处,舰艇B的速度是80海里/小时,请根据以上信息,求舰艇B到达指挥中心O的时间.(结果精确到0.1小时,参考数据:(sin22°≈0.37,cos22°≈0.93,tan22°≈0.40,![]() =1.73)
=1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC看,∠BAC=90°,AC=12,AB=10,D是AC上一个动点,以AD为直径的⊙O交BD于E,则线段CE的最小值是( )

A. 5 B. 6 C. 7 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,y=ax2+bx+c的图象经过点(﹣1,0),(m,0);有如下判断:①abc<0;②b>3c;③![]() =1﹣
=1﹣![]() ;④|am+a|=
;④|am+a|=![]() .其中正确的判断有( )
.其中正确的判断有( )
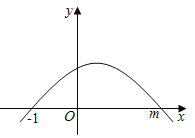
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
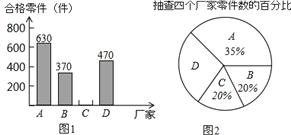
【题目】为响应国家的“一带一路”经济发展战略,树立品牌意识,我市质检部门对A、B、C、D四个厂家生产的同种型号的零件共2000件进行合格率检测,通过检测得出C厂家的合格率为95%,并根据检测数据绘制了如图1、图2两幅不完整的统计图.
(1)抽查D厂家的零件为 件,扇形统计图中D厂家对应的圆心角为 ;
(2)抽查C厂家的合格零件为 件,并将图1补充完整;
(3)通过计算说明合格率排在前两名的是哪两个厂家;
(4)若要从A、B、C、D四个厂家中,随机抽取两个厂家参加德国工业产品博览会,请用“列表法”或“画树形图”的方法求出(3)中两个厂家同时被选中的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知矩形ABCD中,AB=4cm,BC=8cm.动点P在边BC上从点B向C运动,速度为1cm/s;同时动点Q从点C出发,沿折线C→D→A运动,速度为2cm/s.当一个点到达终点时,另一个点随之停止运动。设点P运动的时间为t(s),△BPQ的面积为S(cm2),则描述S(cm2)与时间t(s)的函数关系的图象大致是( )
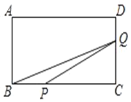
A. B.
B.
C.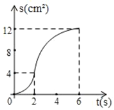 D.
D.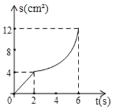
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠ACB=90°,tan∠BAC=![]() . 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
. 点D在边AC上(不与A,C重合),连结BD,F为BD中点.
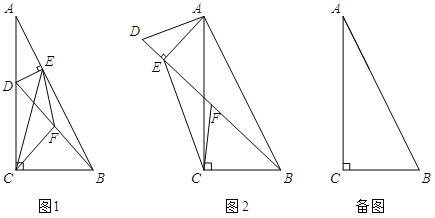
(1)若过点D作DE⊥AB于E,连结CF、EF、CE,如图1.设![]() ,则k= ;
,则k= ;
(2)若将图1中的△ADE绕点A旋转,使得D、E、B三点共线,点F仍为BD中点,如图2所示.求证:BE-DE=2CF;
(3)若BC=6,点D在边AC的三等分点处,将线段AD绕点A旋转,点F始终为BD中点,求线段CF长度的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com