
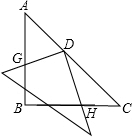
 角形的斜边中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.
角形的斜边中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.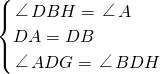 ,
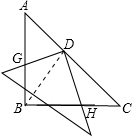
,
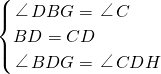 ,
, S△ABC,
S△ABC, S△ABC=4cm2,
S△ABC=4cm2,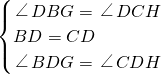 ,
,
 S△ABC,即得,S四边形DGBH=
S△ABC,即得,S四边形DGBH= S△ABC=4cm2,便可确定在旋转过程中四边形GBHD的面积不变;
S△ABC=4cm2,便可确定在旋转过程中四边形GBHD的面积不变;

科目:初中数学 来源: 题型:
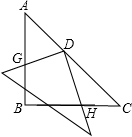 角形的斜边中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.
角形的斜边中点O 处,且可以绕点O旋转,在旋转过程中,两直角边的交点G、H始终在边AB、BC上.查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市潮南区中考模拟考试数学卷 题型:解答题
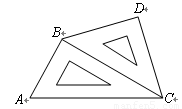
如图小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知 ,求
,求 的长?
的长?
查看答案和解析>>
科目:初中数学 来源:2011年广东省汕头市潮南区中考模拟考试数学卷 题型:解答题
如图小明将一幅三角板如图所示摆放在一起,发现只要知道其中一边的长就可以求出其它各边的长,若已知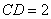 ,求
,求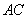 的长?
的长?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com