
分析 设快车的长度为x米,则快车从刚上桥到完全离开桥行驶的路程是(1000+x)米,列快车完全在桥上行驶的路程是(1000-x)米,根据列车的速度不变列出一元一次方程,然后可求得快车的速度,最后设经过y秒快车追上慢车,根据快车的路程-慢车的路程=1500米列方程求解即可.
解答 解:设快车的长度为x米.
根据题意得:$\frac{1000+x}{60}=\frac{1000-x}{40}$
解得:x=200.
$\frac{1000+200}{60}=20$米/秒.
设经过y秒快车追上慢车.
根据题意得:20y-10y=1500.
解得y=150.
答:经过150秒,快车追上慢车.
点评 本题主要考查的是一元一次方程的应用,根据快车的速度不变列出关于x的方程是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.
如图,AB,CD是⊙O的两条直径,过点A作AE∥CD交⊙O于点E,连接BD,DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
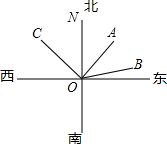 如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.
如图,甲、乙、丙三艘轮船从港口O出发,当分别行驶到A,B,C处时,经测量得,甲船位于港口的北偏东43°45′方向,乙船位于港口的北偏东76°35′方向,丙船位于港口的北偏西43°45′方向.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{-a}$ | B. | -$\sqrt{a}$ | C. | -$\sqrt{-a}$ | D. | $\sqrt{a}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com