
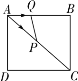
【题目】如图,已知在矩形 ABCD 中,AB=4,AD=3,连接 AC,动点 Q 以每秒 1 个单位的速度沿 A→B→C 向点 C 匀速运动,同时点 P 以每秒 2 个单位的速度沿 A→C→D 向点 D 匀速运动,连接 PQ,当点 P 到达终点 D 时,停止运 动,设△APQ 的面积为 S,运动时间为 t 秒,则 S 与 t 函数关系的图象大致为( )
A.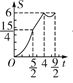 B.
B.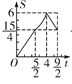 C.
C. D.
D.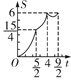
【答案】A
【解析】
根据题意,由矩形的性质和勾股定理,得到AC=5,则得到点P的运动时间为![]() 秒,则对运动过程进行分类讨论:①当点P从点A运动到点C的过程,即
秒,则对运动过程进行分类讨论:①当点P从点A运动到点C的过程,即![]() ;②点P经过点C之后,点Q到达点B时,即
;②点P经过点C之后,点Q到达点B时,即![]() ;③点Q经过点B后,点P到达点D停止,即
;③点Q经过点B后,点P到达点D停止,即![]() ;分别求出S与t的关系,即可得到答案.
;分别求出S与t的关系,即可得到答案.
解:由矩形的性质,得∠B=90°,AB=DC=4,AD=BC=3,
由勾股定理,得:![]() ,
,
∴点P运动到点C的时间为:![]() 秒;
秒;
点P运动到点D的时间为:![]() 秒;
秒;
点Q运动到点B的时间为:![]() 秒;
秒;
根据运动的情况,可分成以下三种情况:
①当点P从点A运动到点C的过程,即![]() ,
,
如图,作PE⊥AB于E,
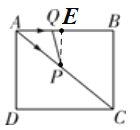
∴![]() ,
,![]() ,
,
∵PE⊥AB,BC⊥AB,
∴△APE∽△ACB,
∴![]() ,
,
∴![]() ,
,
∴△APQ 的面积为:![]() (
(![]() );
);
②点P经过点C之后,点Q到达点B时,即![]() ;
;
如图,
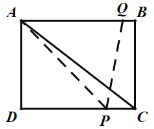
∴△APQ 的面积为:![]() (
(![]() );
);
③点Q经过点B后,点P到达点D停止,即![]() ;如图,
;如图,
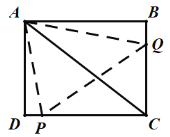
此时,![]() ,
,![]() ,
,
∴![]() ,
,
∴△APQ 的面积为:![]() ,
,
∴![]()
![]()
![]()
![]() (
(![]() );
);
∴S 与 t函数关系的图象大致为A选项中的图像;
故选:A.


科目:初中数学 来源: 题型:
【题目】2020年2月22日深圳地铁10号线华南城站试运行,预计今年6月正式开通.在地铁的建设中,某段轨道的铺设若由甲乙两工程队合做,12天可以完成,共需工程费用27720元;已知乙队单独完成这项工程所需时间是甲队单独完成这项工程所需时间的1.5倍,且甲队每天的工程费用比乙队多250元.
(1)求甲、乙两队单独完成这项工程各需多少天?
(2)若工程管理部门决定从这两个队中选一个队单独完成此项工程,从节约资金的角度考虑,应选择哪个工程队?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角梯形ABCD中,AB∥CD,AD⊥AB,∠B=60°,AB=10,BC=4,点P沿线段AB从点A向点B运动,设AP=x.

(1)求AD的长;
(2)点P在运动过程中,是否存在以A、P、D为顶点的三角形与以P、C、B为顶点的三角形相似?若存在,求出x的值;若不存在,请说明理由;
(3)设△ADP与△PCB的外接圆的面积分别为S1、S2,若S=S1+S2,求S的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
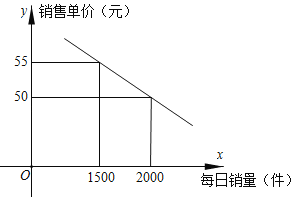
【题目】为倡导节能环保,降低能源消耗,提倡环保型新能源开发,造福社会.某公司研发生产一种新型智能环保节能灯,成本为每件40元.市场调查发现,该智能环保节能灯每件售价y(元)与每天的销售量为x(件)的关系如图,为推广新产品,公司要求每天的销售量不少于1000件,每件利润不低于5元.
(1)求每件销售单价y(元)与每天的销售量为x(件)的函数关系式并直接写出自变量x的取值范围;
(2)设该公司日销售利润为P元,求每天的最大销售利润是多少元?
(3)在试销售过程中,受国家政策扶持,毎销售一件该智能环保节能灯国家给予公司补贴m(m≤40)元.在获得国家每件m元补贴后,公司的日销售利润随日销售量的增大而增大,则m的取值范围是 (直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC,∠B=90゜,AB=3,BC=6,动点P、Q同时从点B出发,动点P沿BA以1个单位长度/秒的速度向点A移动,动点Q沿BC以2个单位长度/秒的速度向点C移动,运动时间为t秒.连接PQ,将△QBP绕点Q顺时针旋转90°得到△![]() ,设△
,设△![]() 与△ABC重合部分面积是S.
与△ABC重合部分面积是S.
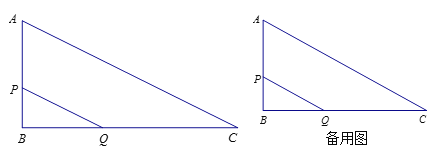
(1)求证:PQ∥AC;
(2)求S与t的函数关系式,并直接写出自变量t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,②分别是某款篮球架的实物图和示意图,已知支架AB的长为2.3m,支架AB与地面的夹角∠BAC=70°,BE的长为1.5m,篮板部支架BD与水平支架BE的夹角为46°,BC、DE垂直于地面,求篮板顶端D到地面的距离.(结果保留一位小数,参考数据:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75,sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
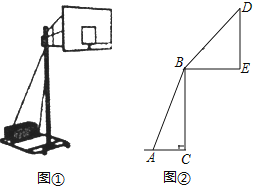
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() .
.
(1)求该函数的图象与x轴的交点坐标.
(2)已知A(-9,![]() ),B(1,
),B(1,![]() ),C(
),C(![]() ,
,![]() )都在该函数的图象上,则
)都在该函数的图象上,则![]() ,
,![]() ,
,![]() 的大小关系为:.
的大小关系为:.
(3)把该函数的图象沿y轴向什么方向平移多少个单位长度后,与x轴只有一个公共点.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图示为一座拱桥,当水面宽AB为12m时,桥洞顶部离水面的距离为2m.
(1)若图中的拱形呈抛物线形状,当水面下降1m后,水面宽为多少?
(2)若图中的拱形呈圆弧形状,当水面下降1m后,水面宽又为多少?
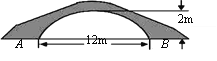
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,荧光屏上的甲、乙两个光斑(可看作点)分别从相距8cm的A,B两点同时开始沿线段AB运动,运动工程中甲光斑与点A的距离S1(cm)与时间t(s)的函数关系图象如图2,乙光斑与点B的距离S2(cm)与时间t(s)的函数关系图象如图3,已知甲光斑全程的平均速度为1.5cm/s,且两图象中△P1O1Q1≌P2Q2O2,下列叙述正确的是( )

A. 甲光斑从点A到点B的运动速度是从点B到点A的运动速度的4倍
B. 乙光斑从点A到B的运动速度小于1.5cm/s
C. 甲乙两光斑全程的平均速度一样
D. 甲乙两光斑在运动过程中共相遇3次
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com