
 如图,△ABC为等边三角形,P为三角形外一点,且∠BAC+∠BPC=180°,求证:PA=PB+PC.
如图,△ABC为等边三角形,P为三角形外一点,且∠BAC+∠BPC=180°,求证:PA=PB+PC. 分析 延长BP至E,使PE=PC,连接CE,证△CPE为等边三角形得CP═PE=CE,再证△ACP≌△BCE得AP=BE,可得PA=PB+PC.
解答 解:如图,延长BP至E,使PE=PC,连接CE,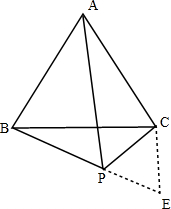
∵∠BAC+∠BPC=180°,且∠BAC=60°,
∴∠BPC=120°,
∴∠CPE=60°,又PE=PC,
∴△CPE为等边三角形,
∴CP=PE=CE,∠PCE=60°,
∵△ABC为等边三角形,
∴AC=BC,∠BCA=60°,
∴∠ACB=∠PCE,
∴∠ACB+∠BCP=∠PCE+∠BCP,
即:∠ACP=∠BCE,
在△ACP和△BCE中,
∵$\left\{\begin{array}{l}{AC=BC}\\{∠ACP=∠BCE}\\{PC=PE}\end{array}\right.$,
∴△ACP≌△BCE(SAS),
∴AP=BE,
∵BE=BP+PE,
∴PA=PB+PC.
点评 本题主要考查全等三角形的判定与性质,通过构建等边三角形为两三角形全等提供条件是关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,点A,D是网格中的两点,现在将点A进行两次平移,第一次平移后的对应点为B第二次平移后的对应点为C,顺次连接ABCD四点,恰好是一个等腰梯形,请你在网格中画出图形,使这个等腰梯形的面积为12.
如图,点A,D是网格中的两点,现在将点A进行两次平移,第一次平移后的对应点为B第二次平移后的对应点为C,顺次连接ABCD四点,恰好是一个等腰梯形,请你在网格中画出图形,使这个等腰梯形的面积为12.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,二次函数y=-$\frac{1}{{m}^{2}}$x2-$\frac{2x}{m}$+3(其中m是常数,且m>0)的图象与x轴交于A、B(点A位于点B的左侧),与y轴交于点C,作CD∥AB,点D在二次函数的图象上,连接BD,过点B作射线BE交二次函数的图象于点E,使得AB平分∠DBE.
如图,二次函数y=-$\frac{1}{{m}^{2}}$x2-$\frac{2x}{m}$+3(其中m是常数,且m>0)的图象与x轴交于A、B(点A位于点B的左侧),与y轴交于点C,作CD∥AB,点D在二次函数的图象上,连接BD,过点B作射线BE交二次函数的图象于点E,使得AB平分∠DBE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:
由于现在人们生活水平的普遍提高,大家对自己的生存环境越来越关注,特别是对大气环境质量的关注,而空气中又以PM2.5对人体的危害性最大,某市环保局对该市市民进行了一项民意调查,以了解PM2.5浓度升高时对人们户外活动是否有影响,并制作了统计图表的一部分如下:| 公众对于户外活动的态度 | 百分比 |
| A.没有影响 | a |
| B.影响不大,还可以进行户外活动 | 5% |
| C.有影响,减少户外活动 | 42% |
| D.影响很大,尽可能不去户外活动 | b |
| E.不关心这个问题 | 6% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE=6,∠ACD=∠B,△ABC的面积为8.
如图,B、C、E三点在同一条直线上,AC∥DE,AC=CE=6,∠ACD=∠B,△ABC的面积为8.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com