
分析 (1)首先重新分组,进而利用提取公因式法分解因式得出即可;
(2)利用十字相乘法分解因式结合待定系数法将原式变形得出答案.
解答 解:(1)ab-2a-b+2
=a(b-2)-(b-2)
=(b-2)(a-1);
(2)x2-xy-2y2-2x+7y-3
=(x-y)(x+2y)+2x+7y-3
用待定系数法
(x-y+m)(x+2y+n)
=(x-y)(x+2y)+n(x-y)+m(x+2y)+mn
=(x-y)(x+2y)+nx-ny+mx+2my+mn
=(x-y)(x+2y)+x(n+m)+y(2m-n)+mn
则m+n=2,2m-n=7,mn=-3
故3m=9
解得:m=3,n=-1,
所以原式=(x-y+m)(x+2y+n)
=(x-y+3)(x+2y-1).
点评 此题主要考查了分组分解法以及十字相乘法,正确分组是解题关键.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:初中数学 来源: 题型:解答题
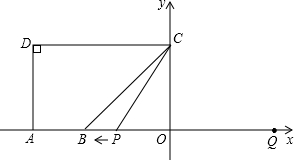 如图,已知A(-5,0)、B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.
如图,已知A(-5,0)、B(-3,0),点C在y轴的正半轴上,∠CBO=45°,CD∥AB,∠CDA=90°点,P从点Q(4,0)出发,沿x轴向左以每秒1个单位长度的速度运动,运动时间ts.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:
我国是世界上严重缺水的国家之一.为了增强居民的节水意识,某市自来水公司对居民用水采用以户为单位分段计费的办法收费.即一个月用水10吨以内(包括10吨)的用户,每吨收水费a元;一个月用水超过10吨的用户,10吨水仍按每吨a元收费,超过10吨的部分,按每吨b元(b>a)收费.设一户居民月用水x吨,应收水费y元,y与x之间的函数关系如图:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com