
【题目】如图①,AE是⊙O的直径,点C是⊙O上的点,连结AC并延长AC至点D,使CD=CA,连结ED交⊙O于点B. 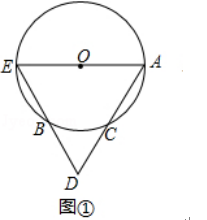
(1)求证:点C是劣弧 ![]() 的中点;
的中点;
(2)如图②,连结EC,若AE=2AC=4,求阴影部分的面积.
【答案】
(1)解:连接CE,
∵AE是⊙O的直径,
∴CE⊥AD,
∵AC=CD,
∴AE=ED,
∴∠AEC=∠DEC,
∴ ![]() ;
;
∴点C是劣弧 ![]() 的中点;
的中点;
(2)连接BC,OB,OC,
∵AE=2AC=4,
∴∠AEC=30°,AE=AD,
∴∠AED=60°,
∴△AED是等边三角形,
∴∠A=60°,
∵ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴AE∥BC,∠BOC=60°,
∴S△OBC=S△EBC,
∴S阴影=S扇形= ![]() =
= ![]() π.
π.
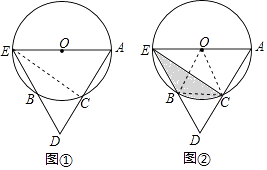
【解析】(1)连接CE,由AE是⊙O的直径,得到CE⊥AD,根据等腰三角形的性质得到∠AEC=∠DEC,于是得到结论;(2)连接BC,OB,OC,由已知条件得到△AED是等边三角形,得到∠A=60°,推出AE∥BC,∠BOC=60°,于是得到结论.
【考点精析】掌握圆周角定理和扇形面积计算公式是解答本题的根本,需要知道顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半;在圆上,由两条半径和一段弧围成的图形叫做扇形;扇形面积S=π(R2-r2).


科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,E、F分别在AD、BC边上,且AE=CF.
求证:(1)△ABE≌△CDF;
(2)四边形BFDE是平行四边形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义函数:在y关于x的函数中,若0≤x≤1时,函数y有最大值和最小值,分别记ymax和ymin , 且满足 ![]() ,则我们称函数y为“三角形函数”.
,则我们称函数y为“三角形函数”.
(1)若函数y=x+a为“三角形函数”,求a的取值范围;
(2)判断函数y=x2﹣ ![]() x+1是否为“三角形函数”,并说明理由;
x+1是否为“三角形函数”,并说明理由;
(3)已知函数y=x2﹣2mx+1,若对于0≤x≤1上的任意三个实数a,b,c所对应的三个函数值都能构成一个三角形的三边长,则求满足条件的m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
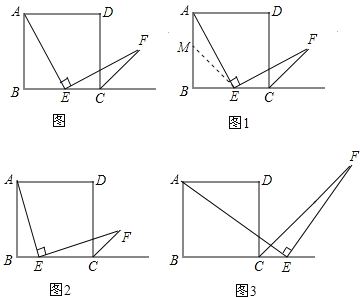
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角平分线CF于点F.请你认真阅读下面关于这个图的探究片段,完成所提出的问题.
(1)探究1:小强看到图(*)后,很快发现AE=EF,这需要证明AE和EF所在的两个三角形全等,但△ABE和△ECF显然不全等(一个是直角三角形,一个是钝角三角形),考虑到点E是边BC的中点,因此可以选取AB的中点M,连接EM后尝试着去证△AEM≌EFC就行了,随即小强写出了如下的证明过程:
证明:如图1,取AB的中点M,连接EM.
∵∠AEF=90°
∴∠FEC+∠AEB=90°
又∵∠EAM+∠AEB=90°
∴∠EAM=∠FEC
∵点E,M分别为正方形的边BC和AB的中点
∴AM=EC
又可知△BME是等腰直角三角形
∴∠AME=135°
又∵CF是正方形外角的平分线
∴∠ECF=135°
∴△AEM≌△EFC(ASA)
∴AE=EF
(2)探究2:小强继续探索,如图2,若把条件“点E是边BC的中点”改为“点E是边BC上的任意一点”,其余条件不变,发现AE=EF仍然成立,请你证明这一结论.
(3)探究3:小强进一步还想试试,如图3,若把条件“点E是边BC的中点”改为“点E是边BC延长线上的一点”,其余条件仍不变,那么结论AE=EF是否成立呢?若成立请你完成证明过程给小强看,若不成立请你说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),在平面直角坐标系中,直线y=﹣![]() x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
x+4交坐标轴于A、B两点,过点C(﹣4,0)作CD⊥AB于D,交y轴于点E.
(1)求证:△COE≌△BOA;
(2)如图2,点M是线段CE上一动点(不与点C、E重合),ON⊥OM交AB于点N,连接MN.
①判断△OMN的形状.并证明;
②当△OCM和△OAN面积相等时,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
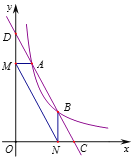
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于C、D两点,与反比例函数
轴交于C、D两点,与反比例函数![]() 的图像相交于点
的图像相交于点![]() 和点
和点![]() ,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
,过点A作AM⊥y轴于点M,过点B作BN⊥x轴于点N,连结MN、OA、OB.下列结论:
①![]() ;②
;②![]() ;③四边形
;③四边形![]() 与四边形MNCA的周长相等;④
与四边形MNCA的周长相等;④![]() .其中正确的个数是( )个.
.其中正确的个数是( )个.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC中,∠ACB=90°,AC=BC= ![]() ,D、E是AB边上的两个动点,满足∠DCE=45°.
,D、E是AB边上的两个动点,满足∠DCE=45°. 
(1)如图②,把△ADC绕着点C顺时针旋转90°,得到△BKC,连结EK. 
①求证:△DCE≌△KCE.
②求证:DE2=AD2+BE2 .
③思考与探究:当点D从点A向AB的中点运动的过程中,请尝试写出DE长度的变化趋势 ![]() ;并直接写出DE长度的最大值或最小值
;并直接写出DE长度的最大值或最小值 ![]() (标明最大值或最小值).
(标明最大值或最小值).
(2)如图③,若△CDE的外接圆⊙O分别交AC,BC于点F、G,求证:CF:CG=BE:AD. 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC.
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.

查看答案和解析>>
科目:初中数学 来源: 题型:
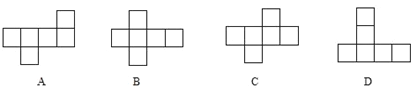
【题目】(1)下面四个图分别由六个相同的正方形拼接而成,其中不能折(从A、B、C、D选择)的是_________.
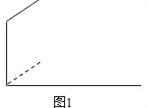
(2)用斜二侧画法补画图1的图形,使之成为长方体的直观图(虚线表示被遮住的线段;只要在已有图形基础上画出长方体,不必写画法步骤).
(3)在这一长方体中,从同一个顶点出发的三个面的面积之比是5:7:2,其中最大的比最小的面积大60cm2,求这个长方体的表面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com