
| A. | $\sqrt{2}$+$\sqrt{3}$=$\sqrt{5}$ | B. | 3$\sqrt{2}$-$\sqrt{2}$=3 | C. | $\sqrt{4\frac{1}{4}}$=2$\frac{1}{2}$ | D. | $\sqrt{(-3)^{2}}$=3 |
分析 分别根据二次根式的加减法与二次根式的化简对各选项进行逐一分析即可.
解答 解:A、$\sqrt{2}$与$\sqrt{3}$不是同类项,不能合并,故本选项错误;
B、3$\sqrt{2}$-$\sqrt{2}$=2$\sqrt{2}$≠3,故本选项错误;
C、$\sqrt{4\frac{1}{4}}$=$\frac{\sqrt{17}}{2}$≠2$\frac{1}{2}$,故本选项错误;
D、$\sqrt{(-3)^{2}}$=3,故本选项正确.
故选D.
点评 本题考查的是二次根式的加减法,熟知二次根式相加减,先把各个二次根式化成最简二次根式,再把被开方数相同的二次根式进行合并,合并方法为系数相加减,根式不变是解答此题的关键.


科目:初中数学 来源: 题型:解答题
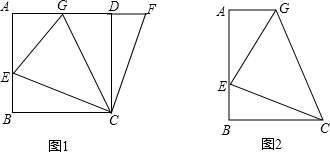
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形,以A为圆心,AB的长为半径画弧交数轴于点C,那么点C在数轴上表示的实数是( )
如图,线段AB边长为1个单位长度的正方形分割为两个等腰直角三角形,以A为圆心,AB的长为半径画弧交数轴于点C,那么点C在数轴上表示的实数是( )| A. | 1+$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\sqrt{2}-1$ | D. | 1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)
如图,在某段测速公路BC上(公路视为直线)交通管理部门规定汽车的最高行驶速度不能超过60千米/时,并在离该公路100米处设置了一个监测点A,已知点B在A的北偏西60°方向上,点C在点A的偏东40°方向上.(1)监测发现,一辆汽车从点B匀速行驶到点C所用时间为15秒.请你通过计算,判断该越野车在这段限速路上是否超速?(参考数据:sin40°=0.64,tan40°=0.84,$\sqrt{3}$=1.73)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 先阅读理解下面的例题,再按要求解答下列问题:
先阅读理解下面的例题,再按要求解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 品种 | 第1年 | 第2年 | 第3年 | 第4年 | 第5 年 |
| 甲 | 9.8 | 9.9 | 10.1 | 10 | 10.2 |
| 乙 | 9.4 | 10.3 | 10.8 | 9.7 | 9.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点A的坐标为(-2,2),点B与点A关于x轴对称,点B先向右平移4个单位长度,再向上平移2个单位长度得到点C.
如图,在平面直角坐标系中,点A的坐标为(-2,2),点B与点A关于x轴对称,点B先向右平移4个单位长度,再向上平移2个单位长度得到点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
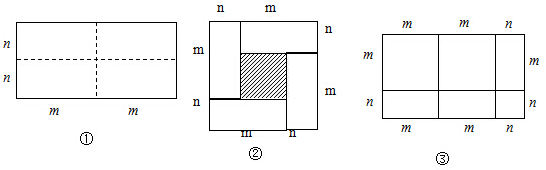
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com