
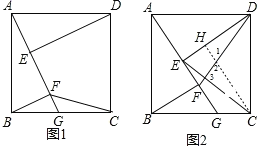
【题目】如图1,四边形ABCD是正方形,AB=4,点G在BC边上,BG=3,DE⊥AG于点E,BF⊥AG于点F.
(1)求BF和DE的长;
(2)如图2,连接DF、CE,探究并证明线段DF与CE的数量关系与位置关系.


【答案】(1)![]() ;(2)DF=CE,DF⊥CE.理由见解析;
;(2)DF=CE,DF⊥CE.理由见解析;
【解析】(1)如图1,先利用勾股定理计算出AG=![]() =5,再利用面积法和勾股定理计算出
=5,再利用面积法和勾股定理计算出![]() 然后证明△ABF≌△DAE,得到DE=AF=
然后证明△ABF≌△DAE,得到DE=AF=![]() ;
;
(2)作CH⊥DE于H,如图2,先利用△ABF≌△DAE,得到![]() 则
则![]() 与(1)的证明方法一样可得△CDH≌△DAE,则
与(1)的证明方法一样可得△CDH≌△DAE,则![]()
![]() 于是可判断EH=EF,接着证明△DEF≌△CHE,所以DF=CE,∠EDF=∠HCE,然后利用三角形内角和得到
于是可判断EH=EF,接着证明△DEF≌△CHE,所以DF=CE,∠EDF=∠HCE,然后利用三角形内角和得到![]() 从而判断DF⊥CE.
从而判断DF⊥CE.
(1)如图1,
∵四边形ABCD是正方形,
∴![]() ,
,
∵DE⊥AG,BF⊥AG,
∴![]()
在Rt△ABG中,AG=![]() =5,
=5,
∵![]()
∴![]()
∴AF=![]() =
=![]() =
=![]() ,
,
∵![]()
∴∠ABF=∠DAE,
在△ABF和△DAE中
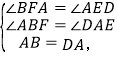
∴△ABF≌△DAE,
∴DE=AF=![]() ;
;
(2)DF=CE,DF⊥CE.理由如下:
作CH⊥DE于H,如图2,
∵△ABF≌△DAE,
∴![]()
∴![]()
与(1)的证明方法一样可得△CDH≌△DAE,
∴![]()
∴![]()
∴EH=EF,
在△DEF和△CHE中
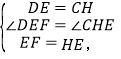
∴△DEF≌△CHE,
∴DF=CE,∠EDF=∠HCE,
∵∠1=∠2,
∴![]()
∴DF⊥CE.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:初中数学 来源: 题型:
【题目】如图所示,已知AB是圆O的直径,圆O过BC的中点D,且DE⊥AC. 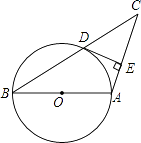
(1)求证:DE是圆O的切线;
(2)若∠C=30°,CD=10cm,求圆O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,点D,E分别是边BC,AB上的中点,连接DE并延长至点F,使EF=2DF,连接CE、AF.
(1)证明:AF=CE;
(2)当∠B=30°时,试判断四边形ACEF的形状并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AD是弦,∠A=22.5°,延长AB到点C,使得∠ACD=45°. 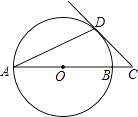
(1)求证:CD是⊙O的切线.
(2)若AB=2 ![]() ,求OC的长.
,求OC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】饮水机接通电源就进入自动程序,开机加热时每分钟上升10℃,加热到100℃,停止加热,水温开始下降,此时水温y(℃)与开机后用时x(min)成反比例关系.直至水温降至20℃时自动开机加热,重复上述自动程序.若在水温为20℃时,接通电源后,水温y(℃)和时间x(min)的关系如图,
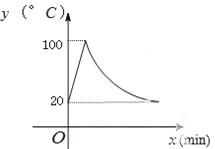
(1) 分别求出直线及双曲线的解析式.
(2) 学生在每次温度升降过程中能喝到50℃以上水的时间有多长?
(3) 若某天上午六点饮水机自动接通电源,问学生上午第一节下课时(8:15)能喝到超过50℃的水吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学八年级的篮球队有![]() 名队员.在罚篮投球训练中,这
名队员.在罚篮投球训练中,这![]() 名队员各投篮
名队员各投篮![]() 次的进球情况如下表:
次的进球情况如下表:
进球数 |
|
|
|
|
|
|
人数 |
|
|
|
|
|
|
针对这次训练,请解答下列问题:
![]() 这
这![]() 名队员进球数的平均数是________,中位数是________;
名队员进球数的平均数是________,中位数是________;
![]() 求这支球队罚篮命中率.罚篮命中率
求这支球队罚篮命中率.罚篮命中率![]() (进球数
(进球数![]() 投篮次数)
投篮次数)![]() ________;
________;
![]() 若队员小亮的罚篮命中率为
若队员小亮的罚篮命中率为![]() ,请你分析小亮在这支球队中的罚篮水平.
,请你分析小亮在这支球队中的罚篮水平.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,BD垂直平分AC,垂足为点F,E为四边形ABCD外一点,且∠ADE=∠BAD,AE⊥AC.
(1)求证:四边形ABDE是平行四边形;
(2)如果DA平分∠BDE,AB=5,AD=6,求AC的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在求1+2+22+23+24+25+26的值时,小明发现:从第二个加数起每一个加数都是前一个加数的2倍,于是他设:S=1+2+22+23+24+25+26①然后在①式的两边都乘以2,得:2S=2+22+23+24+25+26+27 ②;②﹣①得2S﹣S=27﹣1,S=27﹣1,即1+2+22+23+24+25+26=27﹣1.
(1)求1+3+32+33+34+35+36的值;
(2)求1+a+a2+a3+…+a2013(a≠0且a≠1)的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com