练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图，在直径为82cm的圆柱形油槽内装有一些油以后，油面宽AB=80cm，则油的最大深度为（　　）
    A．32cmB．31cmC．9cmD．18cm

    分析 先连接OA，过点O作OC⊥AB，交⊙O于D，根据垂径定理，即可求得AC的值，然后在Rt△OAC中，利用勾股定理，即可求得OC的值，继而求得油的最大深度．

    解答 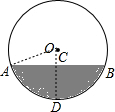解：如图，过O作OC⊥AB于点C，并延长交⊙O于点D，连结OA，
    依题意得CD就是油的最大深度，
    根据垂径定理得：AC=$\frac{1}{2}$AB=40cm，OA=41cm，
    在Rt△OAC中，根据勾股定理得：OC=$\sqrt{O{A}^{2}-A{C}^{2}}$=$\sqrt{4{1}^{2}-4{0}^{2}}$=9（cm），
    ∴CD=OD-OC=41-9=32（cm），
    故选A．

    点评 此题考查了垂径定理的应用．此题难度不大，解题的关键是注意数形结合思想的应用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    17．若两个相似三角形的面积比为1：4，则这两个相似三角形的周长比是1：2．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．解不等式组，并把解集表示在数轴上．
    $\left\{\begin{array}{l}{2x+5≤3（x+2），}&{①}\\{\frac{1-2x}{3}+\frac{1}{5}＞0，}&{②}\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

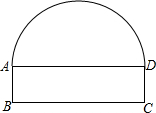    3．如图，隧道的截面由半圆和长方形构成，长方形的长BC为12m，宽AB为3m，若该隧道内设双行道，现有一辆货运卡车高8m，宽2.3m，则这辆货运卡车能否通过该隧道？

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    10．已知⊙O1、⊙O2相交于点A、B，AB=24，O1O2=25，⊙O1半径为20，则⊙O2半径为15．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．已知：如图，两个半径长为r的等圆⊙O1和⊙O2外切于点P，A是⊙O1上的一点，BP⊥AP，BP交⊙O2于点B．求证：AB=2r．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    7．一个圆弧形门拱的拱高为8米，跨度为24米，那么这个门拱的半径为13米．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    4．如图，建筑工人砌墙时，经常在两个墙脚的位置分别插一根木桩，然后拉一条直的参照线，这种做法用几何知识解释应是（　　）
    A．两点之间，线段最短B．射线只有一个端点
    C．两直线相交只有一个交点D．两点确定一条直线

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    5．已知函数y=（m-3）x+n-2（m，n为常数）的图象如图所示，化简：|m-3|-$\sqrt{{n}^{2}-4n+4}$．

    查看答案和解析>>

    同步练习册答案