练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    9．下列命题是真命题的是（　　）
    A．等腰三角形顶角的外角平分线与底边平行
    B．等腰三角形的高、中线、角平分线互相重合
    C．底角相等的两个等腰三角形全等
    D．等腰三角形的一边不可能是另一边的两倍

    分析 根据等腰三角形的性质和平行线的判定对A进行判断；根据等腰三角形“三线合一”对B进行判断；根据全等三角形的判定方法对C进行判断；根据三角形三边的关系对D进行判断．

    解答 解：A、等腰三角形顶角的外角平分线与底边平行，所以A选项为真命题；
    B、等腰三角形的底边上的高、中线和顶角的角平分线互相重合，所以B选项为假命题；
    C、底角相等的两个等腰三角形不一定全等，所以C选项为假命题；
    D、等腰三角形的腰可以为底边的两倍，所以D选项为假命题．
    故选A．

    点评 本题考查了命题与定理：判断一件事情的语句，叫做命题．许多命题都是由题设和结论两部分组成，题设是已知事项，结论是由已知事项推出的事项，一个命题可以写成“如果…那么…”形式． 有些命题的正确性是用推理证实的，这样的真命题叫做定理．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：选择题

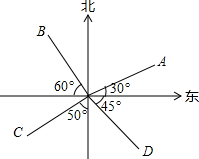    19．如图，下列说法正确的是（　　）
    A．OA的方向是北偏东30°B．OB的方向是北偏西60°
    C．OC的方向是南偏东50°D．OD的方向是东偏南45°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    20．如图，l1∥l2，若∠1=100°，∠2=160°，则∠3为（　　）
    A．60°B．70°C．80°D．90°

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    17．如图，在△ABC中，AB=AC，AD是边BC上的高，E为AC边上一点，且有AE=AD，∠EDC=22°，则∠B的度数为（　　）
    A．44°B．46°C．56°D．54°

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．已知：在△ABC中，AB=AC，AD⊥BC，垂足为D，BE⊥AC，垂足为E，M为AB的中点，联结DE、DM．
    （1）当∠C=70°时（如图），求∠EDM的度数；
    （2）当△ABC是钝角三角形时，请画出相应的图形；设∠C=α，用α表示∠EDM（可直接写出）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    14．直线y=3x-6与x轴交点的坐标是（2，0），与y轴交点的坐标是（0，-6）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    1．如图1，等腰△ABC中，AC=BC=5，AB=$2\sqrt{5}$，O为腰AC上的一个动点，以O为圆心OA为半径作⊙O交AB于点P，PD⊥BC于点D．
    （1）求证：PD为⊙O的切线；
    （2）如图2，当O点运动到⊙O恰好与BC相切时，设切点为E点，连接CP，求tan∠BCP的值．

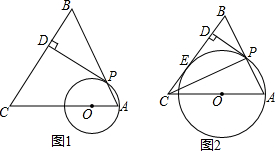
    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    18．分别过△ABC的3个顶点作对边的平行线，这些平行线相交，则可构成（　　）个平行四边形．
    A．1B．2C．3D．4

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    19．若不等式ax＞b的解集是x＞$\frac{b}{a}$，则a的范围是a＞0．

    查看答案和解析>>

    同步练习册答案