
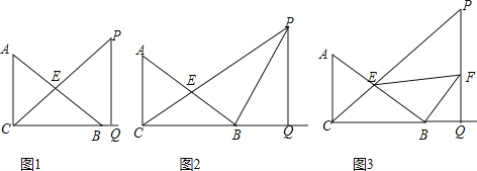
【题目】在△ABC中,∠ACB=90°,点E是斜边AB的中点,AB=10,BC=8,点P在CE的延长线上,过点P作PQ⊥CB,交CB的延长线于点Q,设EP=x
(1)如图1,求证:△ABC∽△PCQ;
(2)如图2,连接PB,当PB平分∠CPQ时,试用含x的代数式表示△PBE的面积;
(3)如图3,过点B作BF⊥AB交PQ于点F.若∠BEF=∠A,试求x的值.
【答案】(1)证明见解析;(2)![]() ;(3)x=10.
;(3)x=10.
【解析】
(1)易证明到∠PQC=∠ACB.即可求证:△ABC∽△PCQ
(2)过点B作BH⊥PC于H,可证BH=BQ,此时根据(1)中:△ABC∽△PCQ,可解得BQ=BH=![]() ,
,![]() 即可求解.
即可求解.
(3)已知BC=8,AB=10,通过证明△ABC∽△BFQ,求出BF,再证△ACB∽△EBF,可得![]() ,即可求出x的值.
,即可求出x的值.
解:(1)∵点E是斜边AB的中点,
∴CE=![]() ,
,
∴∠PCQ=∠ABC
∵PQ⊥CB
∴∠PQC=90°
又∵∠ACB=90°,
∴∠PQC=∠ACB
∴△ABC∽△PCQ
(2)过点B作BH⊥PC于H,
∵BP平分∠CPQ,BH⊥PC,BQ⊥PQ
∴BH=BQ
由(1)知,△ABC∽△PCQ,
∴![]() ,即AB×CQ=BC×PC
,即AB×CQ=BC×PC
而AB=10,BC=8,CQ=BC+BQ=8+BQ,PC=CE+EP=5+x
∴10×(8+BQ)=8×(5+x),解得BQ=![]() ,
,
∴BH=![]()
![]()

(3)∵∠FBQ+∠ABC=90°,∠A+∠ABC=90°
∴∠A=∠FBQ
又∵∠ACB=∠EBF=90°,
∴△ABC∽△BFQ
∴![]() ,即AB×BQ=AC×BF
,即AB×BQ=AC×BF
又由(2)知BQ=![]()
∴![]() =6×BF,解得BF=
=6×BF,解得BF=![]()
∵∠FEB=∠A,∠EBF=∠ACB=90°
∴△ACB∽△EBF
∴![]() ,即
,即![]()
解得x=10


科目:初中数学 来源: 题型:
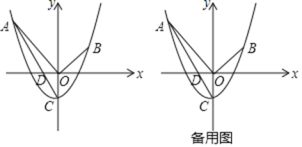
【题目】如图,在平面直角坐标系中,抛物线![]() ,过点
,过点![]() 和点
和点![]() ,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
,与y轴交于点C,连接AC交x轴于点D,连接OA,OB
![]() 求抛物线
求抛物线![]() 的函数表达式;
的函数表达式;
![]() 求点D的坐标;
求点D的坐标;
![]() 的大小是______;
的大小是______;
![]() 将
将![]() 绕点O旋转,旋转后点C的对应点是点
绕点O旋转,旋转后点C的对应点是点![]() ,点D的对应点是点
,点D的对应点是点![]() ,直线
,直线![]() 与直线
与直线![]() 交于点M,在
交于点M,在![]() 旋转过程中,当点M与点
旋转过程中,当点M与点![]() 重合时,请直接写出点M到AB的距离.
重合时,请直接写出点M到AB的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,点D在边BC上,∠CAD=∠B,点E在边AB上,联结CE交AD于点H,点F在CE上,且满足CFCE=CDBC.
(1)求证:△ACF∽△ECA;
(2)当CE平分∠ACB时,求证:![]() =
=![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
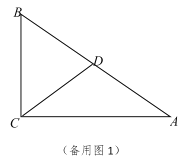
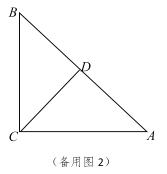
【题目】如图,已知![]() 中,
中,![]() ,
,![]() 是边
是边![]() 的中点,
的中点,![]() 是边
是边![]() 上一动点,
上一动点,![]() 与
与![]() 相交于点
相交于点![]() .
.
(1)如果![]() ,
,![]() ,且
,且![]() 为
为![]() 的中点,求线段
的中点,求线段![]() 的长;
的长;
(2)联结![]() ,如果
,如果![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)联结![]() ,如果
,如果![]() ,且
,且![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
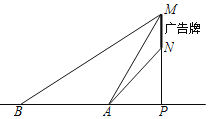
【题目】某数学社团成员想利用所学的知识测量某广告牌的宽度![]() 图中线段MN的长
图中线段MN的长![]() ,直线MN垂直于地面,垂足为点
,直线MN垂直于地面,垂足为点![]() 在地面A处测得点M的仰角为
在地面A处测得点M的仰角为![]() 、点N的仰角为
、点N的仰角为![]() ,在B处测得点M的仰角为
,在B处测得点M的仰角为![]() ,
,![]() 米,且A、B、P三点在一直线上
米,且A、B、P三点在一直线上![]() 请根据以上数据求广告牌的宽MN的长.
请根据以上数据求广告牌的宽MN的长.
![]() 参考数据:
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
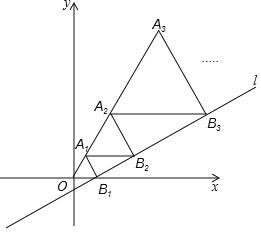
【题目】在直角坐标系中,直线l1:y![]() 与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1,作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3,为边长作等边△A3A2B3…,则等边△A2019A2018B2019的边长是______.
与x轴交于点B1,以OB1为边长作等边△A1OB1,过点A1,作A1B2平行于x轴,交直线l于点B2,以A1B2为边长作等边△A2A1B2,过点A2作A1B2平行于x轴,交直线l于点B3,以A2B3,为边长作等边△A3A2B3…,则等边△A2019A2018B2019的边长是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 交
交![]() 轴于点
轴于点![]() 和点
和点![]() ,交
,交![]() 轴于点
轴于点![]() .
.
(1)求抛物线的函数表达式;
(2)若点![]() 在抛物线上,且
在抛物线上,且![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)如图,设点![]() 是线段
是线段![]() 上的一动点,作
上的一动点,作![]() 轴,交抛物线于点
轴,交抛物线于点![]() ,求线段
,求线段![]() 长度的最大值,并求出
长度的最大值,并求出![]() 面积的最大值.
面积的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以40m/s的速度将小球沿与地面成30°角的方向击出时,小球的飞行路线将是一条抛物线.如果不考虑空气阻力,小球的飞行高度h(单位:m)与飞行时间t(单位:s)之间具有函数关系h=20t﹣5t2.下列叙述正确的是( )

A. 小球的飞行高度不能达到15m
B. 小球的飞行高度可以达到25m
C. 小球从飞出到落地要用时4s
D. 小球飞出1s时的飞行高度为10m
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com