练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】一商店在某一时间以每件a元（a ＞0）的价格卖出两件衣服，其中一件盈利25%，另一件亏损25%.

    （1）当a =100时,分析卖出这两件衣服总的是盈利还是亏损,或是不盈不亏？

    （2）小明发现：不论a为何值，这样卖两件衣服总的都是亏损.请判断“小明发现”是否正确？

    【答案】（1）当a=100时，卖出这两件衣服总的是亏损；（2）小明的发现是正确的.

    【解析】

    （1）设两件衣服每件的成本价格分别是x元，y元，根据题意列出方程，并解出方程，比较总售价和总成本即可；

    （2）分别用a表示出两件的利润，然后相加，再判断总利润的符号即可.

    （1）设两件衣服每件的成本价格分别是x元，y元.

    依题意列方程：

    解得： x=a，y=a.

    当a=100时，x=80，y=133

    80+133=213＞200

    ∴当a=100时，卖出这两件衣服总的是亏损.

    (2)正确.理由如下:

    a-a+a-a=-a ＜0

    故小明的发现是正确的.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】育红学校七年级学生步行到郊外旅行.七(1)班的学生组成前队，步行速度为4km/h，七(2)班的学生组成后队，速度为6km/h.前队出发1h后，后队才出发，同时后队派一名联络员骑自行车在两队之间不间断地来回进行联络，他骑车的速度为12km/h.

    (1)当联络员追上前队时，离出发点多远？

    (2)当联络员追上前队再到后队集合，总共用了多少时间？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

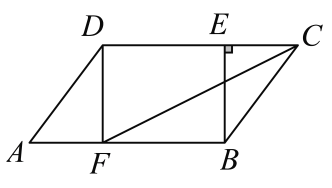
    【题目】在ABCD中，过点B作BE⊥CD于点E，点F在边AB上，AF=CE，连接DF，CF.

    （1）求证：四边形DFBE是矩形；

    （2）当CF平分∠DCB时,若CE=3,BE=4,求CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】我们规定：一组邻边相等且对角互补的四边形叫作“完美四边形”．

    （1）在①平行四边形，②菱形，③矩形，④正方形中，一定为“完美”四边形的是 （请填序号）；

    （2）在“完美”四边形ABCD中，AB=AD，∠B+∠D=180°，连接AC．

    ①如图1，求证：AC平分∠BCD；

    小明通过观察、实验，提出以下两种想法，证明AC平分∠BCD：

    想法一：通过∠B+∠D=180°，可延长CB到E，使BE=CD，通过证明△AEB≌△ACD，从而可证AC平分∠BCD；

    想法二：通过AB=AD，可将△ACD绕点A顺时针旋转，使AD与AB重合，得到△AEB，可证C,B,E三点在条直线上，从而可证AC平分∠BCD.

    请你参考上面的想法，帮助小明证明AC平分∠BCD；

    ②如图2，当∠BAD=90°，用等式表示线段AC,BC,CD之间的数量关系，并证明.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，∠ACB=90°，AC=BC，直线MN经过点C，且AD⊥MN于D，BE⊥MN于E．

    （1）当直线MN绕点C旋转到①的位置时，求证：①△ADC≌△CEB；②DE=AD+BE；

    （2）当直线MN绕点C旋转到②的位置时，求证：DE=AD﹣BE；

    （3）当直线MN绕点C旋转到③的位置时，试问DE、AD、BE具有怎样的数量关系？请直接写出这个等量关系，不需要证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，点A，B是数轴上的两点.点P从原点出发，以每秒2个单位的速度向点B作匀速运动；同时，点Q也从原点出发用2s到达点A处，并在A处停留2s，然后按原速度向点B运动，速度为每秒4个单位.最终，点Q比点P早2s到达B处.设点P运动的时间为ts.

    （1）点A表示的数为 ；当t=4s时，P、Q两点之间的距离为 个单位长度；

    （2）求点B表示的数；

    （3）从P、Q两点同时出发至点P到达点B处的这段时间内，t为何值时，P、Q两点相距3个单位长度？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】用正方形硬纸板做三棱柱盒子，每个盒子由3个矩形侧面和2个正三角形底面组成。硬纸板以如图两种方式裁剪（裁剪后边角料不再利用）

    A方法：剪6个侧面； B方法：剪4个侧面和5个底面。

    现有19张硬纸板，裁剪时张用A方法，其余用B方法。

    （1）用的代数式分别表示裁剪出的侧面和底面的个数；

    （2）若裁剪出的侧面和底面恰好全部用完，问能做多少个盒子？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知A（3，m），B（﹣2，﹣3）是直线AB和某反比例函数的图象的两个交点．

    （1）求直线AB和反比例函数的解析式；

    （2）观察图象，直接写出当x满足什么范围时，直线AB在双曲线的下方；

    （3）反比例函数的图象上是否存在点C，使得△OBC的面积等于△OAB的面积？如果不存在，说明理由；如果存在，求出满足条件的所有点C的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

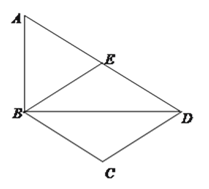
    【题目】如图，在Rt△ABD中，∠ABD=90°，AB=1，sin∠ADB=，点E为AD的中点，线段BA绕点B顺时针旋转到BC（旋转角小于180°），使BC∥AD．连接DC，BE．

    （1）则四边形BCDE是________，并证明你的结论；

    （2）求线段AB旋转过程中扫过的面积．

    查看答案和解析>>

    同步练习册答案