
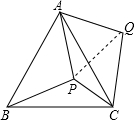
 P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2.
P是等边△ABC内部一点,∠APB、∠BPC、∠CPA的大小之比是5:6:7,将△ABP逆时针旋转,使得AB与AC重合,则以PA、PB、PC的长为边的三角形的三个角∠PCQ:∠QPC:∠PQC=3:4:2. 分析 将△APB绕A点逆时针旋转60°得△AP′C,显然有△AP′C≌△APB,连PP′,则AP′=AP,∠P′AP=60°,得到△AP′P是等边三角形,PP′=AP,所以△P′CP的三边长分别为PA,PB,PC;再由∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=5:6:7,得到∠APB=100°,∠BPC=120°,∠CPA=140°,这样可分别求出∠PP′C=∠AP′C-∠AP′P=∠APB-∠AP′P=100°-60°=40°,∠P′PC=∠APC-∠APP′=140°-60°=80°,∠PCP′=180°-(40°+80°)=60°,即可得到答案.
解答 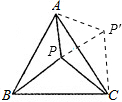 解:如图,将△APB绕A点逆时针旋转60°得△AQC,显然有△AQC≌△APB,连PQ,
解:如图,将△APB绕A点逆时针旋转60°得△AQC,显然有△AQC≌△APB,连PQ,
∵AQ=AP,∠QAP=60°,
∴△AQP是等边三角形,
∴PQ=AP,
∵QC=PB,
∴△QCP的三边长分别为PA,PB,PC,
∵∠APB+∠BPC+∠CPA=360°,∠APB:∠BPC:∠CPA=5:6:7,
∴∠APB=100°,∠BPC=120°,∠CPA=140°,
∴∠PQC=∠AQC-∠AQP=∠APB-∠AQP=100°-60°=40°,
∠QPC=∠APC-∠APQ=140°-60°=80°,
∠PCQ=180°-(40°+80°)=60°,
∴∠PCQ:∠QPC:∠PQC=3:4:2,
故答案为:3:4:2.
点评 本题考查了旋转的性质:旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.也考查了等边三角形的性质,熟记旋转的性质是解题的关键.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
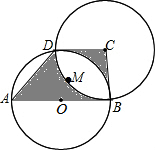 如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:
如图,AB为圆O的直径,点D在圆O上,在梯形ABCD中:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
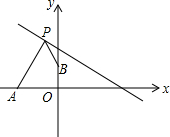 如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).
如图,点A的坐标为(-2,0),点B的坐标为(0,1),点P在直线y=-$\frac{1}{2}$x+2上运动,当线段|AP-BP|最长时,点P的坐标是(1,$\frac{3}{2}$).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 678.89×108元 | B. | 67.889×109元 | C. | 6.7889×109元 | D. | 6.7889×1010元 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x≥$\sqrt{2}$ | B. | x≤$\sqrt{2}$ | C. | x<$\sqrt{2}$ | D. | x>$\sqrt{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
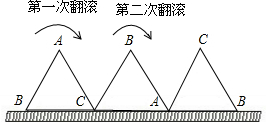 一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.
一块等边三角形木板,边长为1,现将木板沿水平线翻滚,如图所示,若翻滚了2017次,则B点所经过的路径长度为$\frac{2690}{3}$π.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 9$\sqrt{3}$ | B. | 3$\sqrt{3}$ | C. | $\frac{3}{2}$$\sqrt{3}$ | D. | $\frac{1}{4}$$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com