
【题目】如图,![]() 为半圆
为半圆![]() 的直径,
的直径,![]() 交
交![]() 于
于![]() ,
,![]() 为
为![]() 延长线上一动点,
延长线上一动点,![]() 为
为![]() 中点,
中点,![]() ,交半径
,交半径![]() 于
于![]() ,连
,连![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 为定值.其中正确结论的个数为( )
为定值.其中正确结论的个数为( )
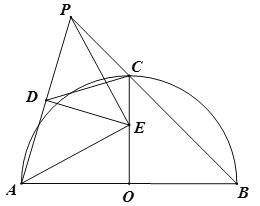
A.1个B.2个C.3个D.4个
【答案】D
【解析】
根据题意可得![]() 是
是![]() 的垂直平分线,
的垂直平分线,![]() 是
是![]() 的垂直平分线,可得点
的垂直平分线,可得点![]() 是
是![]() 的外心,根据圆周角定理可得∠AEP=2∠ABC,进而可判断①;
的外心,根据圆周角定理可得∠AEP=2∠ABC,进而可判断①;
连接AC,如图1,根据圆周角定理的推论并结合①的结论可得点![]() 和点
和点![]() 在以点
在以点![]() 为圆心的同一个圆上,于是可判断②;
为圆心的同一个圆上,于是可判断②;
连接BE,如图2,由①知点![]() 是
是![]() 的外心,然后根据圆周角定理即可判断③;
的外心,然后根据圆周角定理即可判断③;
如图1,在直角![]() 中,利用锐角三角函数和③的结论可得
中,利用锐角三角函数和③的结论可得![]() ,然后将
,然后将![]() 进行整理变形即得结论,进而可判断④,于是可得答案.
进行整理变形即得结论,进而可判断④,于是可得答案.
解:①∵点![]() 是
是![]() 的中点,
的中点,![]() ,∴
,∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∵![]() 是半
是半![]() 的直径,
的直径,![]() ,∴
,∴![]() 是
是![]() 的垂直平分线,
的垂直平分线,
∴点![]() 是
是![]() 的外心,
的外心,
∵![]() ,∴
,∴![]() ,
,
∴![]() ,故①正确;
,故①正确;
②连接AC,如图1,∵![]() 是半
是半![]() 的直径,∴
的直径,∴![]() ,
,
∴点![]() 和点
和点![]() 在以点
在以点![]() 为圆心的同一个圆上,∴
为圆心的同一个圆上,∴![]() ,故②正确;
,故②正确;
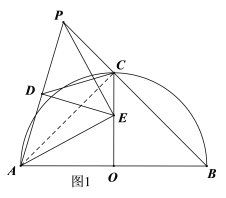
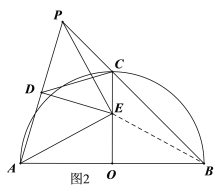
③连接BE,如图2,由①知点![]() 是
是![]() 的外心,∴
的外心,∴![]() ,故③正确;
,故③正确;
④如图1,在直角![]() 中,
中,![]() ,
,
∴![]()
![]() ,
,
∴![]() 为定值,是
为定值,是![]() 半径的
半径的![]() 倍,故④正确.
倍,故④正确.
故选:D.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】反比例函数![]() (
(![]() 为常数.且
为常数.且![]() )的图象经过点
)的图象经过点![]() .
.![]() .
.
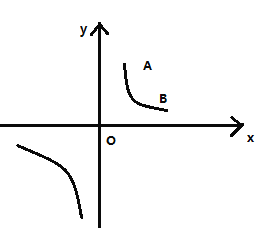
(1)求反比例函数的解析式及![]() 点的坐标;
点的坐标;
(2)在![]() 轴上找一点
轴上找一点![]() .使
.使![]() 的值最小,
的值最小,
①求满足条件的点![]() 的坐标;②求
的坐标;②求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在校园文化艺术节中,九年级一班有1名男生和2名女生获得美术奖,另有1名男生和1名女生获得音乐奖.
(1)从获得美术奖和音乐奖的5名学生中选取1名参加颁奖大会,刚好是男生的概率是 ;
(2)分别从获得美术奖、音乐奖的学生中各选取1名参加颁奖大会,用列表或树状图求刚好是一男生一女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中有4个大小、质地完全相同的乒乓球,球面上分别标有数-1,2,-3,4.
(1)摇匀后任意摸出1个球,则摸出的乒乓球球面上的数是负数的概率为________.
(2)摇匀后先从中任意摸出1个球(不放回),再从余下的3个球中任意摸出1个球,用列表或画树状图的方法求两次摸出的乒乓球球面上的数之和是正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 中,
中,![]() ,
,![]() 的面积为42.
的面积为42.
(1)如图,若点![]() 分别是边
分别是边![]() 的中点,则四边形
的中点,则四边形![]() 的面积是__________.
的面积是__________.

(2)如图,若图中所有的三角形均相似,其中最小的三角形面积为1,则四边形![]() 的面积是___________.
的面积是___________.
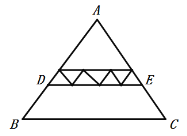
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形![]() 的两边
的两边![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴的正半轴上,
轴的正半轴上,![]() ,
,![]() .点
.点![]() 从点
从点![]() 出发,沿
出发,沿![]() 轴以每秒2个单位长的速度向点
轴以每秒2个单位长的速度向点![]() 匀速运动,当点
匀速运动,当点![]() 到达点
到达点![]() 时停止运动,设点
时停止运动,设点![]() 运动的时间是
运动的时间是![]() 秒.将线段
秒.将线段![]() 的中点绕点
的中点绕点![]() 按顺时针方向旋转
按顺时针方向旋转![]() 得点
得点![]() ,点
,点![]() 随点
随点![]() 的运动而运动,连接
的运动而运动,连接![]() 、
、![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() .
.
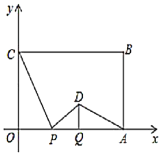
(1)求证:![]() ∽
∽![]() ;
;
(2)请用含![]() 的代数式表示出点
的代数式表示出点![]() 的坐标;
的坐标;
(3)求![]() 为何值时,
为何值时,![]() 的面积最大,最大为多少?
的面积最大,最大为多少?
(4)在点![]() 从
从![]() 向
向![]() 运动的过程中,点
运动的过程中,点![]() 与点
与点![]() 所在的直线能否平分矩形
所在的直线能否平分矩形![]() 的面积?若能,求
的面积?若能,求![]() 的值;若不能,请说明理由.
的值;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形EFGH内接于△ABC,且边FG落在BC上,若AD⊥BC,BC=30,AD=20,EF=![]() EH.
EH.
(1)求证:△AEH∽△ABC;
(2)求矩形EFGH的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市为调查市民上班时最常用的交通工具的情况,随机抽取了部分市民进行调查,要求被调查者从“![]() :自行车,
:自行车,![]() :电动车,
:电动车,![]() :公交车,
:公交车,![]() :家庭汽车,
:家庭汽车,![]() :其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
:其他”五个选项中选择最常用的一项.将所有调查结果整理后绘制成如下不完整的条形统计图和扇形统计图,请结合统计图回答下列问题.
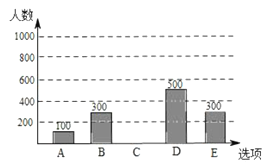
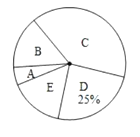
(1)本次调查中,一共调查了 名市民,其中“![]() :公交车”选项的有 人;扇形统计图中,
:公交车”选项的有 人;扇形统计图中,![]() 项对应的扇形圆心角是 度;
项对应的扇形圆心角是 度;
(2)若甲、乙两人上班时从![]() 、
、![]() 、
、![]() 、
、![]() 四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
四种交通工具中随机选择一种,请用列表法或画树状图的方法,求出甲、乙两人恰好选择同一种交通工具上班的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com