
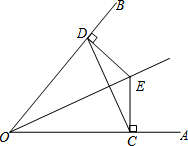
 如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.
如图,E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,垂足分别是C、D.分析 (1)先根据E是∠AOB的平分线上一点,EC⊥OB,ED⊥OA得出△ODE≌△OCE,可得出OC=OD即可;
(2)由等腰三角形的性质即可得出OE是CD的垂直平分线.
解答 证明:∵E是∠AOB的平分线上一点,EC⊥OA,ED⊥OB,
∴DE=CE,OE=OE,
在Rt△ODE与Rt△OCE中,$\left\{\begin{array}{l}{OE=OE}\\{DE=CE}\end{array}\right.$,
∴Rt△ODE≌Rt△OCE(HL),
∴OC=OD;
(2)∵△DOC是等腰三角形,
∵OE是∠AOB的平分线,
∴OE是CD的垂直平分线.
点评 本题考查的是角平分线的性质、全等三角形的判定与性质,证明三角形全等是解决问题的关键.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
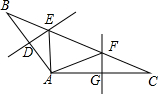 如图,△ABC的周长为30cm,∠BAC=125°,AB+AC=18cm,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.
如图,△ABC的周长为30cm,∠BAC=125°,AB+AC=18cm,AB、AC的垂直平分线分别交BC于E、F,与AB、AC分别交于点D、G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.
如图,在△ABD中,AC⊥BD于C,点E为AC上一点,连结BE、DE,DE的延长线交AB于F,已知DE=AB,∠CAD=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图所示,某规划部门计划将一块长为(3a+b)米,宽为(2a+b)米的长方形地块进行改建,其中阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.
如图所示,某规划部门计划将一块长为(3a+b)米,宽为(2a+b)米的长方形地块进行改建,其中阴影部分进行绿化,中间将修建一座雕像,则绿化的面积是多少平方米?并求出当a=3,b=2时的绿化面积.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com