
”¾ĢāÄæ”æĪŖĮĖĮĖ½āČ«Äź¼¶Ń§ÉśÓ¢Óļ×÷ŅµµÄĶź³ÉĒéæö£¬°ļÖśÓ¢ÓļѧĻ°³É¼Ø²īµÄѧɜ¾”æģĢįø߳ɼأ¬°ąÖ÷ČĪŗĶÓ¢Óļ½ĢŹ¦“ÓČ«Äź¼¶![]() Ćūѧɜ֊³éČ”
Ćūѧɜ֊³éČ”![]() Ćū½ųŠŠµ÷²é£®Ź×ĻČ£¬ĄĻŹ¦¼ģ²éĮĖÕāŠ©Ń§ÉśµÄ×÷Ņµ±¾£¬¼ĒĀ¼ĻĀ»ńµĆ”°ÓÅ”±”¢”°Į¼”±”¢”°ÖŠ”±”¢”°²ī”±µÄČĖŹż±ČĄżĒéæö£»Ęä“ĪĄĻŹ¦·¢øųĆæČĖŅ»Õŵ÷²éĪŹ¾ķ£¬ĘäÖŠÓŠŅ»øöµ÷²éĪŹĢāŹĒ£ŗ”°ÄćµÄÓ¢Óļ×÷ŅµĶź³ÉĒéæöČēŗĪ£æ”±£¬øų³öĪåøöŃ”Ļī£ŗA£®¶ĄĮ¢Ķź³É£»B£®øص¼Ķź³É£»C£®ÓŠŹ±³Ļ®Ķź³É£»D£®¾³£³Ļ®Ķź³É£»E£®¾³£²»Ķź³É£¬¹©Ń§ÉśŃ”Ōń£¬Ó¢Óļ½ĢŹ¦·¢ĻÖŃ”¶ĄĮ¢Ķź³ÉŗĶøص¼Ķź³ÉÕāĮ½ĻīµÄѧɜŅ»¹²Õ¼
Ćū½ųŠŠµ÷²é£®Ź×ĻČ£¬ĄĻŹ¦¼ģ²éĮĖÕāŠ©Ń§ÉśµÄ×÷Ņµ±¾£¬¼ĒĀ¼ĻĀ»ńµĆ”°ÓÅ”±”¢”°Į¼”±”¢”°ÖŠ”±”¢”°²ī”±µÄČĖŹż±ČĄżĒéæö£»Ęä“ĪĄĻŹ¦·¢øųĆæČĖŅ»Õŵ÷²éĪŹ¾ķ£¬ĘäÖŠÓŠŅ»øöµ÷²éĪŹĢāŹĒ£ŗ”°ÄćµÄÓ¢Óļ×÷ŅµĶź³ÉĒéæöČēŗĪ£æ”±£¬øų³öĪåøöŃ”Ļī£ŗA£®¶ĄĮ¢Ķź³É£»B£®øص¼Ķź³É£»C£®ÓŠŹ±³Ļ®Ķź³É£»D£®¾³£³Ļ®Ķź³É£»E£®¾³£²»Ķź³É£¬¹©Ń§ÉśŃ”Ōń£¬Ó¢Óļ½ĢŹ¦·¢ĻÖŃ”¶ĄĮ¢Ķź³ÉŗĶøص¼Ķź³ÉÕāĮ½ĻīµÄѧɜŅ»¹²Õ¼![]() £¬Ć÷ĻŌøßÓŚĖūĘ½Ź±¹Ū²ģµ½µÄ±ČĄż£¬Ēė»Ų“šĻĀĮŠĪŹĢā£ŗ
£¬Ć÷ĻŌøßÓŚĖūĘ½Ź±¹Ū²ģµ½µÄ±ČĄż£¬Ēė»Ų“šĻĀĮŠĪŹĢā£ŗ
£Ø1£©Ó¢Óļ½ĢŹ¦ĖłÓƵĵ÷²é·½Ź½ŹĒ_______£»
£Ø2£©Čē¹ūĄĻŹ¦µÄÓ¢Óļ×÷Ņµ¼ģ²éÖ»µĆ”°²ī”±µÄĶ¬Ń§ÓŠ![]() Ćū£¬ÄĒĆ“¹Ą¼ĘČ«Äź¼¶µÄÓ¢Óļ×÷ŅµÖŠæÉÄÜÓŠ¶ąÉŁĶ¬Ń§µĆ”°²ī”±£»
Ćū£¬ÄĒĆ“¹Ą¼ĘČ«Äź¼¶µÄÓ¢Óļ×÷ŅµÖŠæÉÄÜÓŠ¶ąÉŁĶ¬Ń§µĆ”°²ī”±£»
£Ø3£©ĶعżĪŹ¾ķµ÷²é£¬ĄĻŹ¦µĆµ½µÄŹż¾ŻÓėŹĀŹµ²»·ū£¬ĒėÄć½āŹĶÕāøöĶ³¼ĘŹż×ÖŹ§ÕęµÄŌŅņ£®
”¾“š°ø”æ£Ø1£©³éŃłµ÷²é£»£Ø2£©80ČĖ£»£Ø3£©³Ļ®ŗĶ²»Ķź³É×÷ŅµŹĒ²»ŗĆŠŠĪŖ£¬ÓĀÓŚ³ŠČĻ“ķĪó²»ŹĒĆæøöČĖ¶¼ÄÜ×öµ½µÄ£¬ĖłŅŌ£¬ÕāŃłµÄĪŹĢāÉč¼ĘµĆ²»ŗĆ£¬ÕāŅ²ŹĒµ÷²éČŻŅ׏§ÕęµÄŌŅņ£®
”¾½āĪö”æ
£Ø1£©øł¾Ż“Ó![]() Ćūѧɜ֊³éČ”
Ćūѧɜ֊³éČ”![]() ĆūѧɜæɵĆøƵ÷²é·½Ź½ŹĒ³éŃłµ÷²é£»
ĆūѧɜæɵĆøƵ÷²é·½Ź½ŹĒ³éŃłµ÷²é£»
£Ø2£©ÓĆŃł±¾µÄ²īµÄĒéæö¹Ą¼Ę×ÜĢåµÄ²īµÄČĖŹż¼“æÉ£»
£Ø3£©Ź§ÕęÖ÷ŅŖŌŚÓŚĪŹĢāÉč¼ĘµĆ²»ŗĆ£®
½ā£ŗ£Ø1£©³éŃłµ÷²é£»
£Ø2£©”ß100Ćūѧɜ֊ֻµĆ”°²ī”±µÄĶ¬Ń§ÓŠ8Ćū£¬
”ą1000ĆūѧɜӊµĆ”°²ī”±µÄĪŖ1000”Į![]() £½80£ØČĖ£©£»
£½80£ØČĖ£©£»
£Ø3£©³Ļ®ŗĶ²»Ķź³É×÷ŅµŹĒ²»ŗĆŠŠĪŖ£¬ÓĀÓŚ³ŠČĻ“ķĪó²»ŹĒĆæøöČĖ¶¼ÄÜ×öµ½µÄ£¬ĖłŅŌ£¬ÕāŃłµÄĪŹĢāÉč¼ĘµĆ²»ŗĆ£¬ÕāŅ²ŹĒµ÷²éČŻŅ׏§ÕęµÄŌŅņ£®


 æŖŠÄĮ·Ļ°æĪæĪĮ·Óėµ„ŌŖ¼ģ²āĻµĮŠ“š°ø
æŖŠÄĮ·Ļ°æĪæĪĮ·Óėµ„ŌŖ¼ģ²āĻµĮŠ“š°ø æŖŠÄŹŌ¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
æŖŠÄŹŌ¾ķĘŚÄ©³å“Ģ100·ÖĻµĮŠ“š°ø
| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
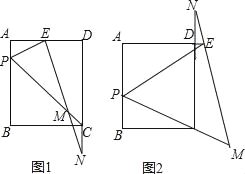
”¾ĢāÄæ”æČēĶ¼1£¬¾ŲŠĪABCDÖŠ£¬PŹĒAB±ßÉĻµÄŅ»µć£Ø²»ÓėA£¬BÖŲŗĻ£©£¬PEĘ½·Ö”ĻAPC½»ÉäĻßADÓŚE£¬¹żE×÷EM”ĶPE½»Ö±ĻßCPÓŚM£¬½»Ö±ĻßCDÓŚN£®
£Ø1£©ĒóÖ¤£ŗCM=CN£»
£Ø2£©ČōAB£ŗBC=4£ŗ3£¬
¢Łµ±![]() =”” ””Ź±£¬EĒ”ŗĆŹĒADµÄÖŠµć£»
=”” ””Ź±£¬EĒ”ŗĆŹĒADµÄÖŠµć£»
¢ŚČēĶ¼2£¬µ±”÷PEMÓė”÷PBCĻąĖĘŹ±£¬Ēó![]() µÄÖµ£®
µÄÖµ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚABCOÖŠ£¬A£Ø1£¬2£©£¬B£Ø5£¬2£©£¬½«ABCOČĘOµćÄꏱÕė·½ĻņŠż×Ŗ90”ćµ½A”äB”äC”äOµÄĪ»ÖĆ£¬ŌņµćB”äµÄ×ų±źŹĒ£Ø””””£©

A.£Ø©2£¬4£©B.£Ø©2£¬5£©C.£Ø©1£¬5£©D.£Ø©1£¬4£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ½«Ņ»ø±Čż½Ē°å£ØÖ±½ĒČż½Ē°åOABŗĶÖ±½ĒČż½Ē°åOCD£¬”ĻAOB=90”ć£¬”ĻABO=45”ć£¬”ĻCDO=90”ć£¬”ĻCOD=60”ć£©
£Ø1£©ČēĶ¼1°Ś·Å£¬µćO”¢A”¢CŌŚŅ»Ö±ĻßÉĻ£¬Ōņ”ĻBODµÄ¶ČŹżŹĒ¶ąÉŁ£æ
£Ø2£©ČēĶ¼2£¬½«Ö±½ĒČż½Ē°åOCDČʵćOÄꏱÕė·½Ļņ×Ŗ¶Æ£¬ČōŅŖOBĒ”ŗĆĘ½·Ö”ĻCOD£¬Ōņ”ĻAOCµÄ¶ČŹżŹĒ¶ąÉŁ£æ
£Ø3£©ČēĶ¼3£¬µ±Čż½Ē°åOCD°Ś·ÅŌŚ”ĻAOBÄŚ²æŹ±£¬×÷ÉäĻßOMĘ½·Ö”ĻAOC£¬ÉäĻßONĘ½·Ö”ĻBOD£¬Čē¹ūČż½Ē°åOCDŌŚ”ĻAOBÄŚČʵćOČĪŅā×Ŗ¶Æ£¬”ĻMONµÄ¶ČŹżŹĒ·ń·¢Éś±ä»Æ£æČē¹ū²»±ä£¬ĒóĘäÖµ£»Čē¹ū±ä»Æ£¬ĖµĆ÷ĄķÓÉ£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy=ax2+bx+c£Øa”Ł0£©µÄ¶Ō³ĘÖįĪŖÖ±Ļßx=1£¬ÓėxÖįµÄŅ»øö½»µć×ų±źĪŖ£Ø©1£¬0£©£¬Ęä²æ·ÖĶ¼ĻóČēĶ¼ĖłŹ¾£¬ĻĀĮŠ½įĀŪ£ŗ¢Łb2©4ac£¼0£»¢Ś·½³Ģax2+bx+c=0µÄĮ½øöøłŹĒx1=©1£¬x2=3£»¢Ū2a+b=0£»¢Üµ±y£¾0Ź±£¬xµÄȔֵ·¶Ī§ŹĒ©1£¼x£¼3£»¢Żµ±x£¾0Ź±£¬yĖęxŌö“ó¶ų¼õŠ”£®ĘäÖŠ½įĀŪÕżČ·µÄøöŹżŹĒ£Ø £©
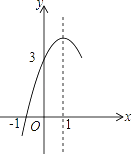
A. 4øö B. 3øö C. 2øö D. 1øö
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
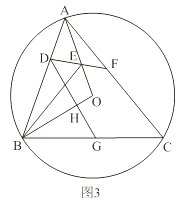
”¾ĢāÄæ”æÓŠĮ½øöÄŚ½Ē·Ö±šŹĒĖüĆĒ¶Ō½ĒµÄŅ»°ėµÄĖıߊĪ½Š×ö°ė¶Ō½ĒĖıߊĪ£®
£Ø1£©ČēĶ¼1£¬ŌŚ°ė¶Ō½ĒĖıߊĪABCDÖŠ£¬”ĻB£½![]() ”ĻD£¬”ĻC£½
”ĻD£¬”ĻC£½![]() ”ĻA£¬Ēó”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ£»
”ĻA£¬Ēó”ĻBÓė”ĻCµÄ¶ČŹżÖ®ŗĶ£»

£Ø2£©ČēĶ¼2£¬Čń½Ē”÷ABCÄŚ½ÓÓŚ”ŃO£¬Čō±ßABÉĻ“ęŌŚŅ»µćD£¬Ź¹µĆBD£½BO£®”ĻOBAµÄĘ½·ÖĻß½»OAÓŚµćE£¬Į¬½įDE²¢ŃÓ³¤½»ACÓŚµćF£¬”ĻAFE£½2”ĻEAF£®

ĒóÖ¤£ŗĖıߊĪDBCFŹĒ°ė¶Ō½ĒĖıߊĪ£»
£Ø3£©ČēĶ¼3£¬ŌŚ£Ø2£©µÄĢõ¼žĻĀ£¬¹żµćD×÷DG”ĶOBÓŚµćH£¬½»BCÓŚµćG£®µ±DH£½BGŹ±£¬Ēó”÷BGHÓė”÷ABCµÄĆ껿֮±Č£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy£½£x2£2x£«3µÄĶ¼ĻóÓėxÖį½»ÓŚA”¢BĮ½µć(µćAŌŚµćBµÄ×ó±ß)£¬ÓėyÖį½»ÓŚµćC£¬µćDĪŖÅ×ĪļĻߵĶ„µć£®
(1)ĒóµćA”¢B”¢CµÄ×ų±ź£»
(2)µćMĪŖĻ߶ĪABÉĻŅ»µć(µćM²»ÓėµćA”¢BÖŲŗĻ)£¬¹żµćM×÷xÖįµÄ“¹Ļߣ¬ÓėÖ±ĻßAC½»ÓŚµćE£¬ÓėÅ×ĪļĻß½»ÓŚµćP£¬¹żµćP×÷PQ”ĪAB½»Å×ĪļĻßÓŚµćQ£¬¹żµćQ×÷QN”ĶxÖįÓŚµćN£¬ČōµćPŌŚµćQ×ó±ß£¬µ±¾ŲŠĪPMNQµÄÖܳ¤×ī“óŹ±£¬Ēó”÷AEMµÄĆ껿£»
(3)ŌŚ(2)µÄĢõ¼žĻĀ£¬µ±¾ŲŠĪPMNQµÄÖܳ¤×ī“óŹ±£¬Į¬½ÓDQ£¬¹żÅ×ĪļĻßÉĻŅ»µćF×÷
yÖįµÄĘ½ŠŠĻߣ¬ÓėÖ±ĻßAC½»ÓŚµćG(µćGŌŚµćFµÄÉĻ·½)£®Čō£¬ ![]()
ĒóµćFµÄ×ų±ź£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖÉäĻßACŹĒ”ĻMANµÄ½ĒĘ½·ÖĻߣ¬ ”ĻNAC=60”ć, B, D·Ö±šŹĒÉäĻßAN. AMÉĻµÄµć£¬Į¬½ÓBD.
(1)ŌŚĶ¼¢ŁÖŠ£¬Čō”ĻABC=”ĻADC=90”ć,Ēó”ĻCDBµÄ“󊔣»
(2)ŌŚĶ¼¢ŚÖŠ£¬Čō”ĻABC+”ĻADC=180”ć,ĒóÖ¤£ŗĖıߊĪABCDµÄĆ껿ŹĒøö¶ØÖµ.

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ĖıߊĪABCDÖŠ£¬”ĻBAD=100”ć£¬”ĻBCD=70”ć£¬µćM£¬N·Ö±šŌŚAB£¬BCÉĻ£¬½«”÷BMNŃŲMN·ÕŪ£¬µĆ”÷FMN£¬ČōMF”ĪAD£¬FN”ĪDC£¬Ēó”ĻBµÄ¶ČŹż£®

²éæ““š°øŗĶ½āĪö>>
°Ł¶ČÖĀŠÅ - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com