
 |
| BC |
 |
| BD |
 |
| CD |
 |
| BC |
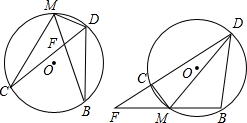 延长线交于点F,连接MC,MD,BD,则结论MC•MD=MF•MB是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由.
延长线交于点F,连接MC,MD,BD,则结论MC•MD=MF•MB是否仍然成立?如果成立,请写出证明过程;如果不成立,请说明理由. 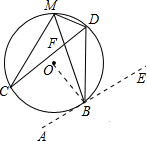 解:(1)如图,正确作出切线.
解:(1)如图,正确作出切线. |
| BC |
 |
| BD |
 |
| BC |
 |
| BD |
| MC |
| MB |
| MF |
| MD |
 |
| BC |
 |
| BD |
| MC |
| MB |
| MF |
| MD |


 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
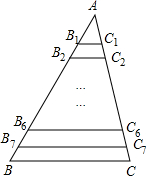 如图,在△ABC中,BC=8,B1、B2、…、B1,C1、C2、…、C7分别是AB、AC的8等分点,则B1C1+B2C2+…+B7C7的值是( )
如图,在△ABC中,BC=8,B1、B2、…、B1,C1、C2、…、C7分别是AB、AC的8等分点,则B1C1+B2C2+…+B7C7的值是( )| A、24 | B、28 | C、32 | D、40 |
查看答案和解析>>
科目:初中数学 来源: 题型:
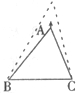 14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )
14、如图,在△ABC中,BC边不动,点A竖直向上运动,∠A越来越小,∠B,∠C越来越大.若∠A减小x°,∠B增加y°,∠C增加z°,则x,y,z之间的关系是( )查看答案和解析>>
科目:初中数学 来源: 题型:
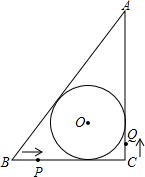 拓展探索.
拓展探索.查看答案和解析>>
科目:初中数学 来源: 题型:
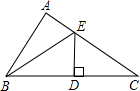 如图,在△ABC中,BC边上的垂直平分线DE交BC于点D,交AC于点E,△ABC的周长为18cm,△ABE的周长为10cm,则BD的长为
如图,在△ABC中,BC边上的垂直平分线DE交BC于点D,交AC于点E,△ABC的周长为18cm,△ABE的周长为10cm,则BD的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com