
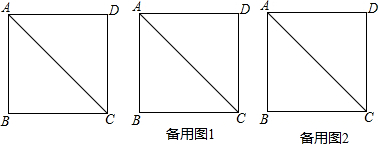
分析 (1)过点P作MN∥BC,分别交AB、CD于点M、N,根据矩形的性质和直角三角形的性质,可证明△QNP≌△PMB,可证明PQ=PB;
(2)设AP=x,结合(1)的结论可分别表示出AM、BM、CQ和PN,可表示出△PBC和△PCQ的面积,从而表示出四边形PBCQ的面积,从而得到y与x的关系式;
(3)△PCQ可以成为等腰三角形.当点Q在DC边上时,利用勾股定理可得到x的方程;当点Q在DC的延长线上时,由PQ=CQ,可得到x的方程;当Q与点C重合时,不满足条件;从而可求得满足条件的x的值,
解答 (1)证明:过点P作MN∥BC,分别交AB、CD于点M、N,如图1,
则四边形AMND和四边形BCNM都是矩形,△AMP和△CNP都是等腰三角形,
∴NP=NC=MB.
∵∠BPQ=90°,
∴∠QPN+∠BPM=90°,而∠BPM+∠PBM=90°,
∴∠QPN=∠PBM.
又∵∠QNP=∠PMB=90°
在△QNP和△PMB中,
$\left\{\begin{array}{l}{∠QPN=∠PBM}\\{NP=MB}\\{∠QNP=∠PMB}\end{array}\right.$,
∴△QNP≌△PMB(ASA),
∴PQ=PB;
(2)解:由(1)知△QNP≌△PMB,得NQ=MP.
设AP=x,则AM=MP=NQ=DN=$\frac{\sqrt{2}}{2}$x,BM=PN=CN=1-$\frac{\sqrt{2}}{2}$x,
∴CQ=CD-DQ=1-2×$\frac{\sqrt{2}}{2}$x=1-$\sqrt{2}$x
∴S△PBC=$\frac{1}{2}$BC•BM=$\frac{1}{2}$×1×(1-$\frac{\sqrt{2}}{2}$x)=$\frac{1}{2}$-$\frac{\sqrt{2}}{4}$x,
S△PCQ=$\frac{1}{2}$CQ•PN=$\frac{1}{2}$×(1-$\sqrt{2}$x)(1-$\frac{\sqrt{2}}{2}$x)=$\frac{1}{2}$-$\frac{3\sqrt{2}}{4}$x+$\frac{1}{2}$x2,
∴S四边形PBCQ=S△PBC+S△PCQ=$\frac{1}{2}$x2-$\sqrt{2}$x+1,
∵当Q点到点C时则P点到达AC的中点,
∴AP的最大值为$\frac{1}{2}$AC=$\frac{\sqrt{2}}{2}$,
∴y=$\frac{1}{2}$x2-$\sqrt{2}$x+1(0≤x<$\frac{\sqrt{2}}{2}$).
(3)△PCQ可能成为等腰三角形.
①当点Q在边DC上,
由PQ2=CQ2得:(1-$\frac{\sqrt{2}}{2}$x)2+($\frac{\sqrt{2}}{2}$x)2=(1-$\sqrt{2}$x)2
解得x1=0,x2=$\sqrt{2}$(舍去);
②当点Q在边DC的延长线上时,如图2,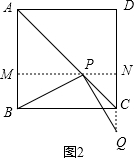
由PC=CQ得:$\sqrt{2}$-x=$\sqrt{2}$x-1,解得x=1.
③当点Q与C点重合,△PCQ不存在.
综上所述,x=0或1时,△PCQ为等腰三角形.
点评 本题主要考查四边形的综合应用,涉及正方形的性质、全等三角形的判定和性质、直角三角形的性质、等腰三角形的性质和勾股定理等知识.在(1)中构造三角形全等是解题的关键,在(2)中用x分别表示出△PBC和△PCQ的面积是解题的关键,在(3)中利用分类讨论思想分别得到关于x的方程是解题的关键.本题考查知识点较多,综合性较强,有一定的难度.


 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案科目:初中数学 来源: 题型:选择题
| A. | 两组对边分别平行 | B. | 一组对边平行且相等 | ||
| C. | 一组对边平行,另一组对边相等 | D. | 两组对边分别相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x>-4 | B. | x<-4 | C. | x>3 | D. | x<3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com