
如图,某小区广场要设计一个矩形花坛,花坛的长、宽分别为30 m、20 m,花坛中有一横一纵的两条通道,余下部分种植花卉.横纵通道的宽度均为x m.
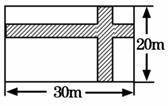
(1)求两条通道的总面积S与x的函数关系式,不要求写出自变量x的取值范围;
(2)当种植花卉面为551米2时,求横、纵通道的宽度为多少米?
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
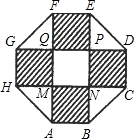 某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图,其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.
某住宅小区,为美化环境,提高居民生活质量,要建一个八边形居民广场(平面图如图,其中,正方形MNPQ与四个相同矩形(图中阴影部分)的面积的和为800m2.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源:《22.3 实际问题与一元二次方程》2009年同步练习(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2011年湖北省鄂州市燕矶中学中考数学模拟试卷(解析版) 题型:解答题

查看答案和解析>>
科目:初中数学 来源:2004年云南省中考数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com