
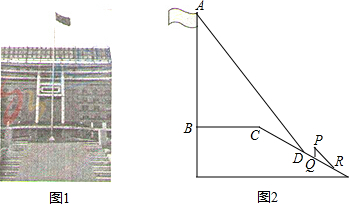
分析 如图作CM∥AB交AD于M,MN⊥AB于N,根据 $\frac{CM}{CD}$=$\frac{PQ}{QR}$,求出CM,在RT△AMN中利用tan72°=$\frac{AN}{MN}$,求出AN即可解决问题.
解答 解:如图,作CM∥AB交AD于点M,MN⊥AB于点N.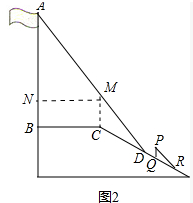
由题意$\frac{CM}{CD}$=$\frac{PQ}{QR}$,即$\frac{CM}{3}$=$\frac{1}{2}$,
∴CM=(米),
在Rt△AMN中,∵∠ANM=90°,MN=BC=4米,∠AMN=72°,
∴tan 72°=$\frac{AN}{MN}$,
∴AN=MN•tan 72°≈4×3.08≈12.3(米).
∵MN∥BC,AB∥CM,
∴四边形MNBC是平行四边形,
∴BN=CM=米,
∴AB=AN+BN=13.8米.
点评 本题考查解直角三角形、三角函数,影长等知识,解题的关键是正确添加辅助线,构造直角三角形解决问题,属于中考常考题型.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:选择题
| A. | k<2,m>0 | B. | k<2,m<0 | C. | k>2,m>0 | D. | k<0,m<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
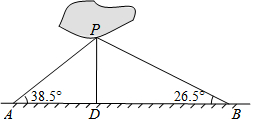 如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)
如图,商丘市睢阳区南湖中有一小岛,湖边有一条笔直的观光小道,现决定从小岛架一座与观光小道垂直的小桥PD,小坤在小道上测得如下数据:AB=200.0米,∠PAB=38.5°,∠PBA=26.5°.请帮助小坤求出小桥PD的长.(结果精确到0.1米)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com