
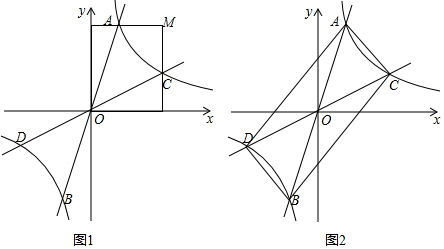
���� ��1������A��B����ԭ��Գƣ��г����̼��ɽ�����⣻
��2������S��OAC=S����OHMG-S��AOG-S��OCH-S��AMC���㼴�ɽ�����⣻
��3��������ͼ2�У���AG��y����G��CH��x����H����֪A��C����ֱ��y=x�Գƣ��Ƴ���AOG�ա�COH���Ƴ�AG=CH��OG=OH����A��m��n��zeBra��n��m�����Ƴ�ֱ��OA�Ľ���ʽΪy=$\frac{n}{m}$x��ֱ��OC�Ľ���ʽΪy=$\frac{m}{n}$x���ɴ˼��ɽ�����⣻
����ͼ2�У���AN��x����N����CD��K������֤��S��AOC=S����ANCH���ɴ��г����̼��ɽ�����⣻
��� �⣺��1���ߵ�A��B������ֱ�Ϊ��1��a2������-1��4-4a����
��A��B����ԭ��Գƣ�
��a2-4a+4=0��
��a=2��
��A��1��4����
��A��1��4������y=$\frac{k}{x}$�У��ɵ�k=4��
��2����ͼ1�У���MA��y����G��MC��x����H������AC��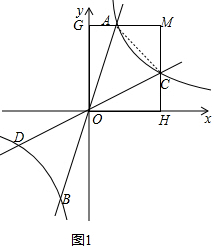
��k=8��M��4��5������A��$\frac{8}{5}$��5����C��4��2����
��AG=$\frac{8}{5}$��AM=$\frac{12}{5}$��CH=2��CM=3��
��S��OAC=S����OHMG-S��AOG-S��OCH-S��AMC=20-$\frac{1}{2}$��5��$\frac{8}{5}$-$\frac{1}{2}$��4��2-$\frac{1}{2}$•$\frac{12}{5}$•3=$\frac{42}{5}$��
��3������ͼ2�У���AG��y����G��CH��x����H��
���ı���ADBC�Ǿ��Σ�
��OA=OC��
��A��C��y=$\frac{k}{x}$�ϣ�����������y=$\frac{k}{x}$�ǹ���ֱ��y=x�ԳƵģ�
��A��C����ֱ��y=x�Գƣ���֪��AOG�ա�COH��
��AG=CH��OG=OH��
��A��m��n��zeBra��n��m����
��ֱ��OA�Ľ���ʽΪy=$\frac{n}{m}$x��ֱ��OC�Ľ���ʽΪy=$\frac{m}{n}$x��
��k1=$\frac{n}{m}$��k2=$\frac{m}{n}$��
��k1•k2=1��
����ͼ2�У���AN��x����N����CD��K��
��S��AON=S��COH��
��S��AOK=S�ı���CHNK��
��S��AOC=S����ANCH��
��A��m��4����C��4��m����
��$\frac{1}{2}$•��4+m��•��4-m��=$\frac{1}{4}$��16��
���m=2$\sqrt{2}$��-2$\sqrt{2}$����������
��A��2$\sqrt{2}$��4����
��k=8$\sqrt{2}$��
���� ���⿼�鷴���������ۺ��⡢��Գơ����ĶԳƵ����ʡ����ε��ж������ʵ�֪ʶ������Ĺؼ������������ѧ֪ʶ������⣬ѧ���÷ָ�������ѧ����ת����˼��˼�����⣬ѧ�ṹ�����̽�����⣬�����п�ѹ���⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
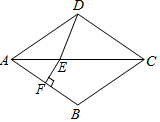 ��ͼ��������ABCD�У���BAD=80�㣬AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�E����AB�ڵ�F������DE�����CDE=60�㣮
��ͼ��������ABCD�У���BAD=80�㣬AB�Ĵ�ֱƽ���߽��Խ���AC�ڵ�E����AB�ڵ�F������DE�����CDE=60�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -$\frac{1}{3}$ | B�� | $\frac{3}{4}$ | C�� | 4 | D�� | $\frac{4}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
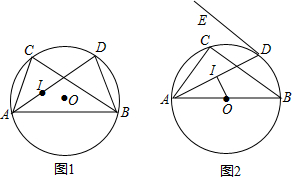
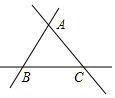 ��ͼ��������ֱ�Ĺ�·AB��AC��BC�����ཻΧ��һ�������εĽ������أ�������Ҫ�ڽ��������⽨һ��ɳʯ��תվ��ʹ��תվ��������·�ľ�����ȣ�����תվ�ɹ�ѡ���λ���У�����������
��ͼ��������ֱ�Ĺ�·AB��AC��BC�����ཻΧ��һ�������εĽ������أ�������Ҫ�ڽ��������⽨һ��ɳʯ��תվ��ʹ��תվ��������·�ľ�����ȣ�����תվ�ɹ�ѡ���λ���У�����������| A�� | 1 | B�� | 2 | C�� | 3 | D�� | 4 |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com