
在一次实践活动中,某课题学习小组用测倾器、皮尺测量旗杆的高度,他们设计了如下方案(如下图所示).
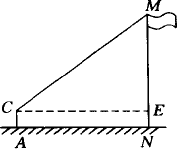
①在测点A处安置测倾器,测得旗杆顶部M的仰角∠MCE=α;
②量出测点A到旗杆底部N的水平距离AN=m;
③量出测倾器的高度AC=h;
根据上述测量数据,即可求出旗杆的高度MN.
如果测量工具不变,请仿照上述过程设计一下测量某小山高度的方案.
(1)在下图中画出你测量小山高度MN的示意图(标上适当字母);
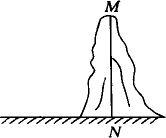
(2)写出你设计的方案.
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 (2010•太原二模)在一次实践活动中,某课题学习小组用测角器、皮尺测量旗杆的高度,在点C处安置测角器,测得旗杆顶部M的仰角∠MCE=60°,量出点A到旗杆底部N的水平距离AN=10m,测角器的高AC=l.3m.请根据上述测量数据,求出旗杆的高度(结果保留两个有效数字).
(2010•太原二模)在一次实践活动中,某课题学习小组用测角器、皮尺测量旗杆的高度,在点C处安置测角器,测得旗杆顶部M的仰角∠MCE=60°,量出点A到旗杆底部N的水平距离AN=10m,测角器的高AC=l.3m.请根据上述测量数据,求出旗杆的高度(结果保留两个有效数字).| 2 |
| 3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
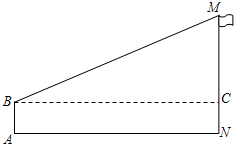 在一次实践活动中,某课堂学习小组用测倾器,皮尺测量旗杆的高度,他们进行了如下的测量(如图所示):
在一次实践活动中,某课堂学习小组用测倾器,皮尺测量旗杆的高度,他们进行了如下的测量(如图所示):查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com