
如图,矩形ABCD中,AB="10" cm,BC="6" cm.现有两个动点P,Q分别从A,B同时出发,点P在线段AB上沿AB方向作匀速运动,点Q在线段BC上沿BC方向作匀速运动,已知点P的运动速度为1 cm/s,运动时间为t s.

(1)设点Q的运动速度为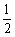 cm/s.
cm/s.
①当△DPQ的面积最小时,求t的值;
②当△DAP∽△QBP相似时,求t的值.
(2)设点Q的运动速度为a cm/s,问是否存在a的值,使得△DAP与△PBQ和△QCD这两个三角形都相似?若存在,请求出a的值;若不存在,请说明理由.
(1)①t="6" ②t=-6+2 (2)①a=
(2)①a=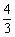
【解析】
试题分析:(1)①S△DPQ=S矩形ABCD-S△DAP-S△PBQ-S△QCD
=60- ×6×t-
×6×t- ×(10-t)×
×(10-t)× t-
t- ×10×(6-
×10×(6- t)
t)
=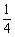 t2-3t+30
t2-3t+30
=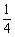 (t-6)2+21.
(t-6)2+21.
∵0≤t≤10,∴当t="6" s时,S△DPQ的最小值为21 cm2.
②当△DAP∽△QBP相似时,有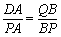 .
.
即 ,解得t1=-6+2
,解得t1=-6+2 ,t2=-6-2
,t2=-6-2 (舍去).
(舍去).
∴t=-6+2 时,△DAP∽△QBP.
时,△DAP∽△QBP.
(2)假设存在a的值,使得△DAP与△PBQ和△QCD这两个三角形都相似,

则AP=t,AQ=at.以下分4种情况进行讨论.
①当∠1=∠3=∠4时,有 .
.
∴ ,解得t1=2,t2=18(舍去).
,解得t1=2,t2=18(舍去).
此时a=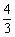 .
.
②当∠1=∠3=∠5时,有∠DPQ=∠PQD=∠PDQ=90°.
此等式不成立.∴不存在这样的a值.
③当∠1=∠2=∠4时,有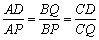 .
.
∴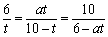 ,即有
,即有 整理,得5t2-36+180=0,△<0,方程无实数解.
整理,得5t2-36+180=0,△<0,方程无实数解.
∴不存在这样的a值.
④当∠1=∠2=∠5时,∵AB∥DC,∴∠1=∠PDC>∠5.故不存在这样的a值.
综上所述,存在a的值,使得△DAP与△PBQ和△QCD这两个三角形都相似,此时a=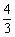
考点:几何图形与代数相结合,相似三角形
点评:该题分析时较为复杂,以图形的边长为路程,分析时间的变动,以及角的变化,是常考题。


科目:初中数学 来源: 题型:
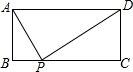 如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )
如图,矩形ABCD中,AD=a,AB=b,要使BC边上至少存在一点P,使△ABP、△APD、△CDP两两相似,则a、b间的关系式一定满足( )A、a≥
| ||
| B、a≥b | ||
C、a≥
| ||
| D、a≥2b |
查看答案和解析>>
科目:初中数学 来源: 题型:
 (2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为
(2008•怀柔区二模)已知如图,矩形ABCD中,AB=3cm,BC=4cm,E是边AD上一点,且BE=ED,P是对角线上任意一点,PF⊥BE,PG⊥AD,垂足分别为F、G.则PF+PG的长为查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com