
 ��k��0����ͼ�����E��ֱ��l1�ཻ�ڵ�F��
��k��0����ͼ�����E��ֱ��l1�ཻ�ڵ�F��
 PE•PF=
PE•PF= ��
�� ��1����k��2��=
��1����k��2��= k2��k+1��
k2��k+1�� •k����
•k���� k2��k+1����k=
k2��k+1����k= k2��1
k2��1 k2��1=2��
k2��1=2�� k2��k+1����
k2��k+1����
 =
= ��
�� ��FM=PF=2��k��
��FM=PF=2��k�� =
= ��BM=
��BM= ��
�� ��2=��
��2=�� ��2+��
��2+�� ��2��
��2�� ����ʱE������Ϊ��
����ʱE������Ϊ�� ��2����
��2����
 =
= ��
�� ��1��
��1�� =
= ��BM=2��
��BM=2�� ��2+22�����k=
��2+22�����k= ��0����k=0���������⣬
��0����k=0���������⣬ ��
�� ��2����
��2���� ��2����
��2���� ��2����
��2����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ������ ���ͣ������
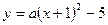 , C2:
, C2: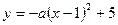 ,C1��C2�Ľ���ΪA,
,C1��C2�Ľ���ΪA,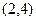 ,��B�ĺ������ǣ�2.
,��B�ĺ������ǣ�2.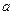 ��ֵ����B�����ꣻ
��ֵ����B�����ꣻ 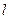 ,��
,��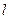 ��x�ύ�ڵ�N.
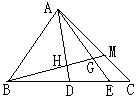
��x�ύ�ڵ�N.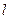 ����DHG�Ķ���G,��D������Ϊ(1, 2)�����N�ĺ����ꣻ
����DHG�Ķ���G,��D������Ϊ(1, 2)�����N�ĺ����ꣻ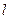 ���DHG�ı�DG�ཻ,���N�ĺ������ȡֵ��Χ.
���DHG�ı�DG�ཻ,���N�ĺ������ȡֵ��Χ.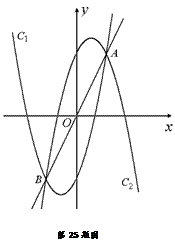
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
| A��1��2 | B��1��4 | C��2��1 | D��4��1 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
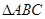 �У�
�� ��
��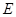 ��
��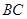 ���ϵĵ㣬
���ϵĵ㣬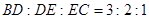 ��
��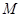 ��
��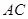
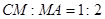 ��
��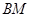 ��
��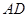 ��
��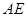 ��
�� ��
�� ����
����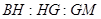 ���� ( )
���� ( )
A��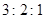 | B��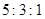 | C��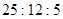 | D�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
 ����OD��
����OD�� =
= 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ���ѡ��
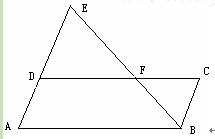
A��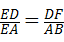 | B��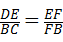 |
C��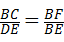 | D��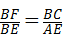 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| AF |
| FD |
| 2 |
| 3 |
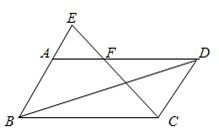
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com