
【题目】如图,已知∠MAN=120°,AC平分∠MAN,∠ABC+∠ADC=180°,求证:①DC=BC; ②AD+AB=AC.
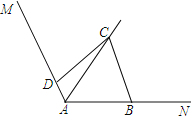
【答案】见解析
【解析】
试题分析:①在AN上截取AE=AC,连接CE,先证明△ACE是等边三角形,得出∠AEC=60°,AC=EC=AE,再证明△ADC≌△EBC,得出DC=BC即可;
②由全等三角形的性质得出AD=BE,即可得出结论.
证明:①在AN上截取AE=AC,连接CE,如图所示:
∵AC平分∠MAN,∠MAN=120°,
∴∠CAB=∠CAD=60°,
∴△ACE是等边三角形,
∴∠AEC=60°,AC=EC=AE,
又∵∠ABC+∠ADC=180°,∠ABC+∠EBC=180°,
∴∠ADC=∠EBC,
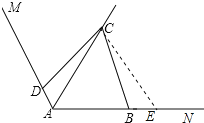
在△ADC和△EBC中,
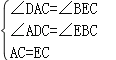 ,
,
∴△ADC≌△EBC(AAS),
∴DC=BC,AD=BE;
②由①得:AD=BE,
∴AB+AD=AB+BE=AE,
∴AB+AD=AC.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】若关于x的一元二次方程(m+1)x2-2x+1=0有实数根,则实数m的取值范围是( )
A、m≥0 B、m≤0 C、m≠1 D、m≤0且m≠-1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列能平方差公式计算的式子是( )
A. (a﹣b)(b﹣a) B. (﹣x+1)(x﹣1)
C. (﹣a﹣1)(a+1) D. (﹣x﹣y)(﹣x+y)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,将一副直角三角板放在同一条直线AB上,其中∠ONM=30°,∠OCD=45°.
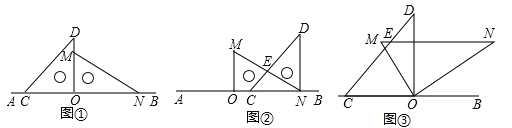
(1)将图①中的三角板OMN沿BA的方向平移至图②的位置,MN与CD相交于点E,求∠CEN的度数;
(2)将图①中的三角板OMN绕点O按逆时针方向旋转至如图③,当∠CON=5∠DOM时,MN与CD相交于点E,请你判断MN与BC的位置关系,并求∠CEN的度数;
(3)将图①中的三角板OMN绕点O按每秒5°的速度按逆时针方向旋转一周,在旋转的过程中,三角板MON运动几秒后直线MN恰好与直线CD平行.
(4)将如图①位置的两块三角板同时绕点O逆时针旋转,速度分别每秒20°和每秒10°,当其中一个三角板回到初始位置时,两块三角板同时停止转动.经过___________秒后边OC与边ON互相垂直.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为( )

A.3cm B.6cm C.![]() cm D.
cm D.![]() cm
cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com